Lei dos Senos
A Lei dos Senos é uma das principais relações da trigonometria e conecta os lados de um triângulo com o seno de seus ângulos. Essa lei é útil para calcular lados e ângulos em qualquer triângulo, inclusive em situações em que não se pode aplicar o Teorema de Pitágoras diretamente.
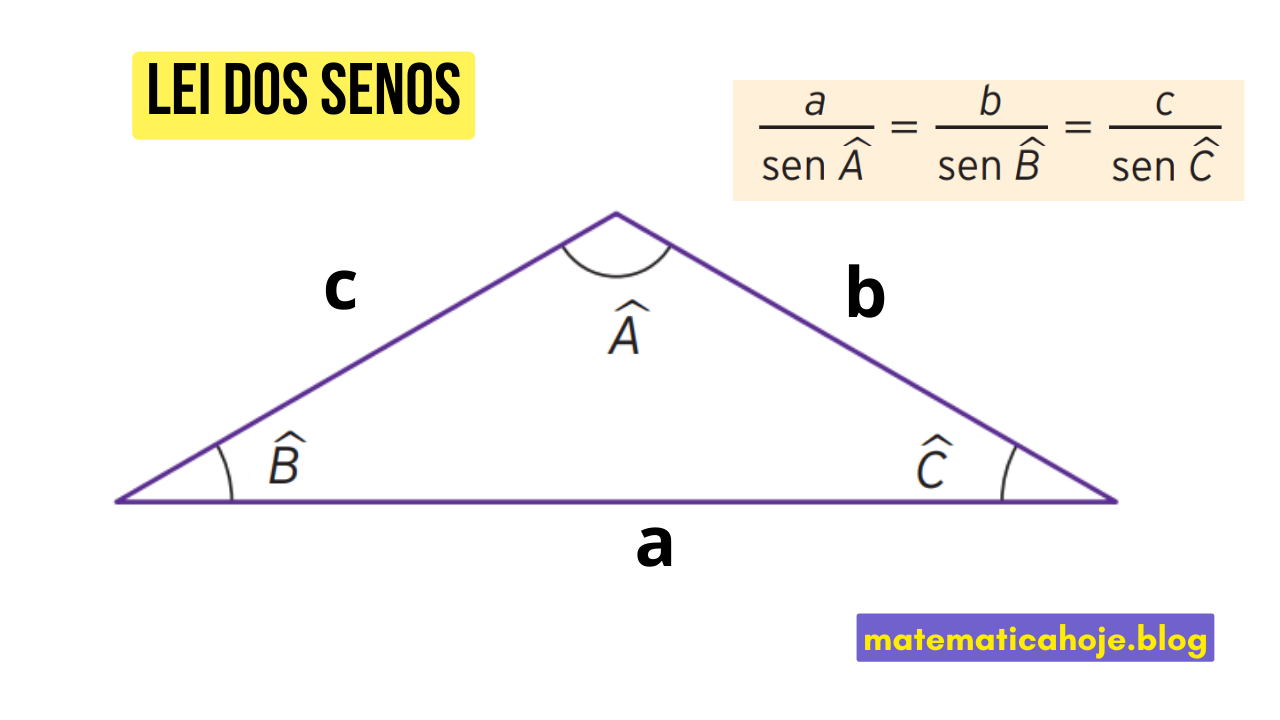
Fórmula da Lei dos Senos
Onde:
- \(a, b, c\) são os lados do triângulo.
- \(\hat{A}, \hat{B}, \hat{C}\) são os ângulos opostos a esses lados.
Demonstração da Lei dos Senos
Considere um triângulo qualquer \(ABC\). Se traçarmos a altura relativa a um dos lados, podemos relacionar os catetos formados com o seno dos ângulos. Assim, demonstramos que a razão entre um lado e o seno do ângulo oposto é constante para os três lados.
Exemplo resolvido
Exemplo: Em um triângulo \(ABC\), sabemos que \(\hat{A} = 40^\circ\), \(\hat{B} = 75^\circ\) e \(a = 10\). Determine o lado \(b\).
Solução:
Primeiro, calcule o terceiro ângulo: \(\hat{C} = 180^\circ – (40^\circ + 75^\circ) = 65^\circ\).
Pela Lei dos Senos: \(\dfrac{a}{\sin \hat{A}} = \dfrac{b}{\sin \hat{B}}\). Substituindo: \(\dfrac{10}{\sin 40^\circ} = \dfrac{b}{\sin 75^\circ}\).
\(b = \dfrac{10 \cdot \sin 75^\circ}{\sin 40^\circ} \approx 15,3\).
Exercícios de prática
1) Num triângulo, temos \(\hat{A} = 60^\circ\), \(\hat{B} = 45^\circ\) e lado \(a = 12\). Qual o valor aproximado do lado \(b\)?
- 10,1
- 11,3
- 13,8
- 15,5
Ver solução
\(\hat{C} = 75^\circ\). Pela Lei dos Senos: \(\dfrac{a}{\sin 60^\circ} = \dfrac{b}{\sin 45^\circ}\). \(b = \dfrac{12 \cdot \sin 45^\circ}{\sin 60^\circ} \approx 13,8\).
2) Em um triângulo, \(\hat{A} = 50^\circ\), \(\hat{C} = 70^\circ\) e \(a = 8\). Determine o lado \(c\).
- 7,5
- 9,4
- 10,1
- 11,2
Ver solução
\(\hat{B} = 60^\circ\). Pela Lei dos Senos: \(\dfrac{a}{\sin 50^\circ} = \dfrac{c}{\sin 70^\circ}\). \(c = \dfrac{8 \cdot \sin 70^\circ}{\sin 50^\circ} \approx 9,4\).






















