Lei dos Senos: como aplicar a fórmula em triângulos qualquer?
A Lei dos Senos é uma das relações fundamentais da Trigonometria e aparece em praticamente todos os contextos envolvendo triângulos: geometria plana, problemas reais, navegação, engenharia e, claro, nas provas de vestibulares como ENEM, ESA, IFRN, ITA, UNICAMP e outros.
Neste artigo você vai aprender o que é a Lei dos Senos, por que ela funciona, como aplicá-la para encontrar lados ou ângulos e verá exemplos resolvidos passo a passo. Além disso, deixei uma lista de exercícios com gabarito em sistema abre/fecha para você treinar — ideal para estudar de forma mais eficiente.
Aproveite também para baixar gratuitamente o eBook de Fórmulas Matemáticas, que reúne as relações mais cobradas em provas:
eBook Fórmulas Matemática
Como entender a relação entre lados e ângulos na Lei dos Senos
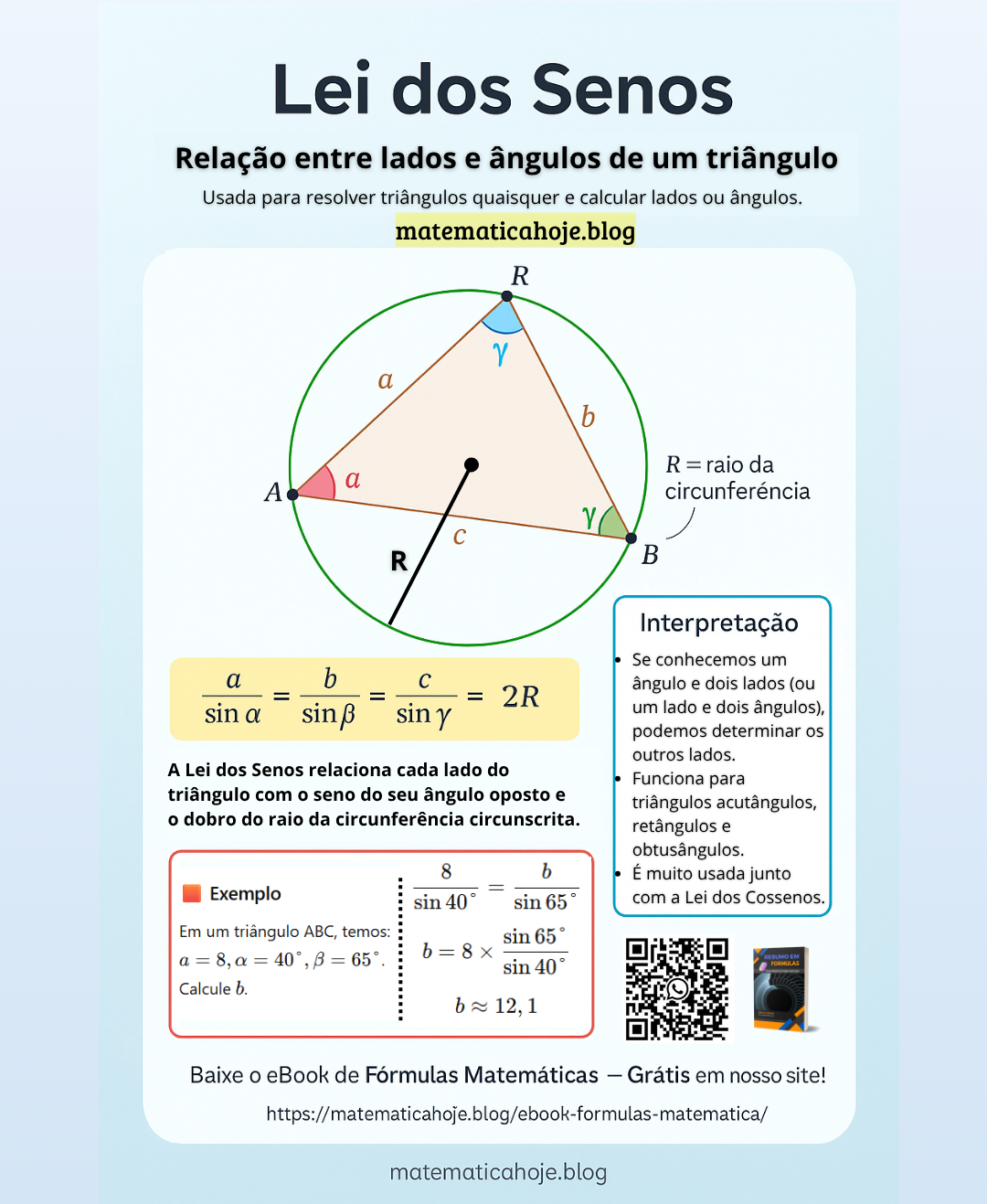
A Lei dos Senos relaciona cada lado do triângulo com o seno de seu ângulo oposto. Em qualquer triângulo (acutângulo, retângulo ou obtusângulo), vale a igualdade:
\[ \frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2R \]
Onde:
- a, b, c são os lados do triângulo;
- α, β, γ são os ângulos opostos a cada lado;
- R é o raio da circunferência circunscrita.
Quando usar a Lei dos Senos?
Ela é ideal nas situações:
- quando temos um lado + ângulo oposto (caso ALO);
- quando temos dois ângulos + um lado (pois a soma dos ângulos é 180°);
- quando precisamos encontrar o raio da circunferência circunscrita.
Mapas Mentais de Matemática
Exemplo resolvido usando a Lei dos Senos passo a passo
Exemplo 1 — Encontrando um lado desconhecido
Enunciado:
Em um triângulo ABC, temos:
- a = 8
- α = 40°
- β = 65°
Calcule o valor de b.
Solução:
\[ \frac{8}{\sin 40^\circ} = \frac{b}{\sin 65^\circ} \]
\[ b = 8 \cdot \frac{\sin 65^\circ}{\sin 40^\circ} \]
Resposta: \( b \approx 12{,}1 \)
Domine rapidamente fórmulas essenciais como Lei dos Senos, Cossenos, áreas e muito mais.
👉 Baixe aqui o eBook de Fórmulas Matemáticas (Grátis)
Aplicações práticas e exemplos úteis com Lei dos Senos
Navegação, distâncias e triangulação
A Lei dos Senos é muito usada em cálculos de localização, engenharia e geodésia, pois permite determinar distâncias inacessíveis apenas medindo ângulos.
Questões de ENEM e vestibulares
Em provas, normalmente aparece vinculada a problemas práticos, como determinação de alturas, larguras, sombras, distâncias ou medidas inclinadas.
Acesse também:
Lista de exercícios — Lei dos Senos
Resolva e depois confira a solução no botão abaixo de cada questão.
✅ Exercício 1
Num triângulo, temos: a = 12 cm, α = 50°, β = 60°. Calcule o lado b.
Mostrar solução
\[ \frac{12}{\sin 50^\circ} = \frac{b}{\sin 60^\circ} \] \[ b = 12 \cdot \frac{\sin 60^\circ}{\sin 50^\circ} \] \[ b \approx 14{,}7\text{ cm} \]
✅ Exercício 2
Em um triângulo, γ = 40°, c = 9 cm e β = 85°. Calcule b.
Mostrar solução
\[ \frac{b}{\sin 85^\circ} = \frac{9}{\sin 40^\circ} \] \[ b = 9 \cdot \frac{\sin 85^\circ}{\sin 40^\circ} \] \[ b \approx 14{,}0\text{ cm} \]
✅ Exercício 3
Determine o raio circunscrito R de um triângulo onde a = 10 e α = 30°.
Mostrar solução
\[ \frac{a}{\sin\alpha} = 2R \] \[ \frac{10}{\sin 30^\circ} = 2R \] \[ \frac{10}{0.5} = 2R \] \[ 20 = 2R \Rightarrow R = 10 \]
Conclusão — o que você aprendeu sobre a Lei dos Senos
Agora você domina a Lei dos Senos: sabe identificar quando utilizar, como aplicar e resolver problemas práticos. Com os exemplos deste artigo, mais a lista de exercícios e o eBook gratuito, você está pronto para resolver triângulos de qualquer tipo — e com confiança.
Continue explorando outros conteúdos de trigonometria no blog e fortaleça sua base para provas, concursos e vestibulares.
FAQ — Perguntas frequentes sobre a Lei dos Senos
Para que serve a Lei dos Senos em problemas de triângulos?
Ela permite encontrar lados e ângulos desconhecidos quando temos um lado e seu ângulo oposto ou quando possuímos dois ângulos e um lado. É útil em problemas de navegação, engenharia e provas como ENEM, ITA e concursos militares.
Qual a diferença entre Lei dos Senos e Lei dos Cossenos?
A Lei dos Senos envolve razões entre lados e senos dos ângulos opostos. Já a Lei dos Cossenos é uma generalização do Teorema de Pitágoras e funciona bem para casos com lado entre dois ângulos. Ambas se complementam na resolução de triângulos.
É possível usar a Lei dos Senos em triângulos retângulos?
Sim. Embora o triângulo retângulo já possua relações diretas, a Lei dos Senos continua válida e pode ser útil para determinar lados quando apenas alguns ângulos são conhecidos.
Quando devo preferir a Lei dos Cossenos à Lei dos Senos?
Use a Lei dos Cossenos quando você conhecer dois lados e o ângulo entre eles (caso LAL) ou quando todos os lados forem conhecidos (LLL). Ela é ideal para situações onde a Lei dos Senos não fornece diretamente a solução.
Autor: Adriano Rocha — matematicahoje.blog





















