Exercício 1 – Em cada item, calcule o valor de x e classifique o triângulo em relação aos ângulos
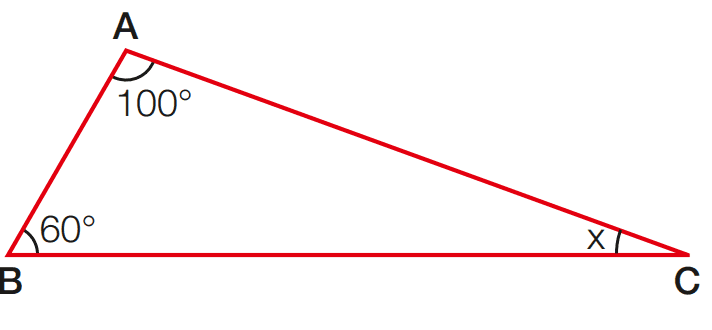
a)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 100 + 60 + x = 180
x = 180 – 100 – 60 = 20
Resposta: x = 20°; triângulo obtusângulo
[/toggle]
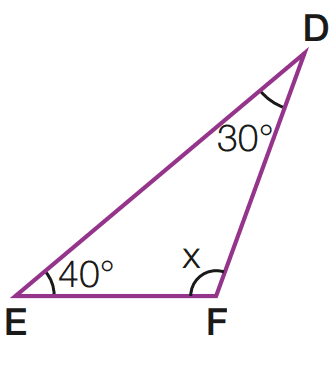
b)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 40 + 30 + x = 180
x = 180 – 40 – 30 = 110
x = 110
Resposta: x = 110°; triângulo obtusângulo
[/toggle]
c)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Temos que 90 + 40 + x = 180
x = 180 – 90 – 40 = 50
x = 50
Resposta: x = 50°; triângulo retângulo
[/toggle]
Exercício 2: Qual é o valor de x?
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Pelo teorema do ângulo externo temos
x = 20 + 30
x = 50°
[/toggle]
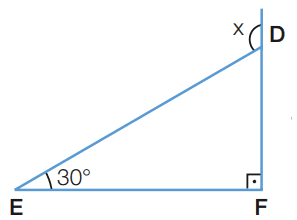
b)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Pelo teorema do ângulo externo temos:
x = 30 + 90
x = 120°
[/toggle]
c)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
2x − 10 = x + y
Onde y = 180 − (2x + 10)
E, usando as propriedades dos ângulos e a soma dos ângulos internos de um triângulo (que somam 180), você chegou à seguinte equação:
2x − 10 = x + 180 − (2x + 10)
A partir dessa equação, o desenvolvimento correto leva ao valor final de:
3x = 180 ⟹ x = 60
Portanto, o valor correto de x é, de fato, 60 graus.
[/toggle]
Exercício 3: Calcule a soma x + y + z nos seguintes casos:
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Utilizando suplemento de cada ângulo temos:
180 – x + 180 – y + 180 – z = 180
x – y – z + 540 = 180
x – y – z = 180 – 540
x – y – z = – 360 x(-1)
x + y + z = 360
[/toggle]
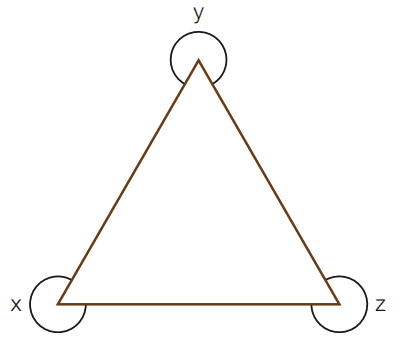
b)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
360 – x + 360 -y +360 – z = 180
1080 – x – y – z = 180
x – y – z = 180 – 1080
x – y – z = -900
x + y + z = 900
[/toggle]
Exercício 4: Determine os valores de x e y em cada item
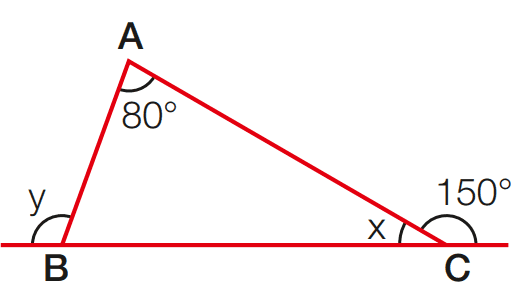
a)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 180 – 150
x = 30
y = 80 + 30
y = 110
[/toggle]
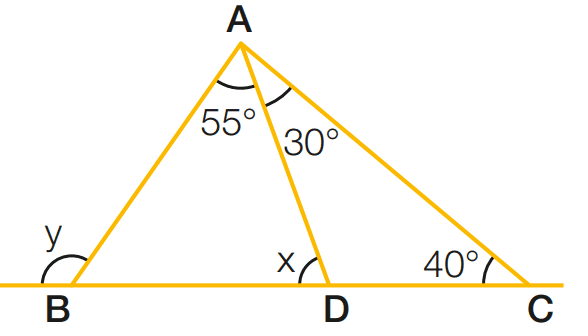
b)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 30 + 40
x = 70
y = 55 + 70
y = 175
[/toggle]
Exercício 5: Sabendo que r // s, calcule o valor de x.
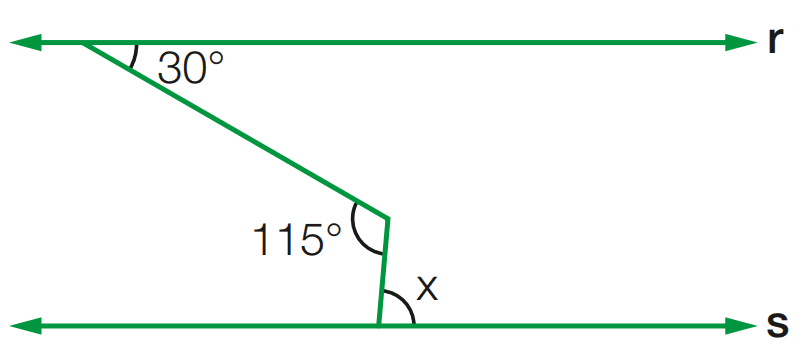
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
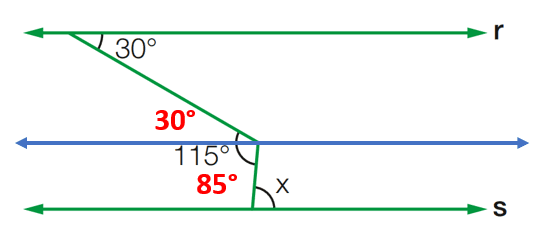
x = 85
[/toggle]
Exercício 6: Na figura, r é paralela a s. Determine a soma x + y.
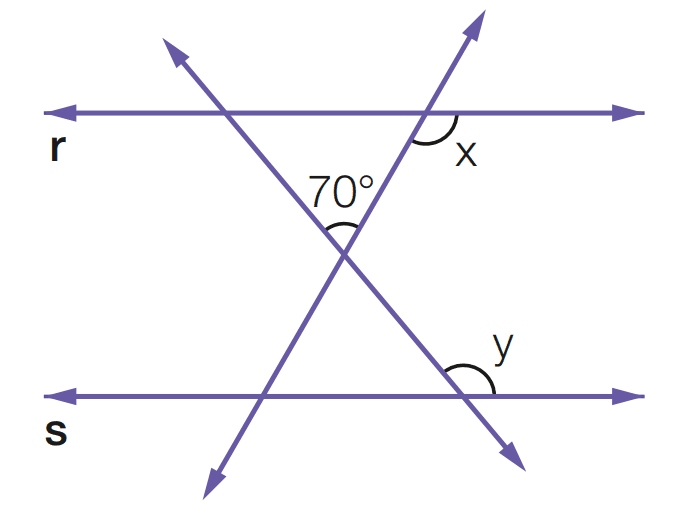
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
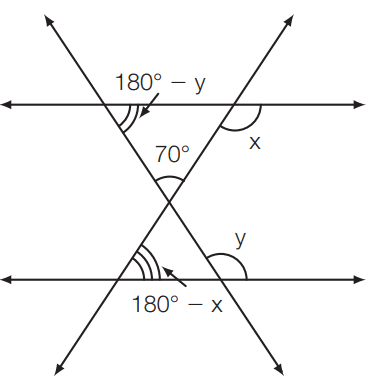
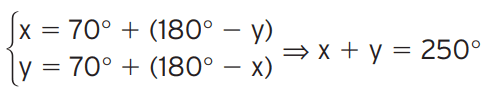
[/toggle]
Exercício 7: Pode-se dizer que existe um triângulo que seja:
a) acutângulo e isósceles?
b) obtusângulo e isósceles?
c) retângulo e isósceles?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
a) Sim.
b) Sim.
c) Sim.
[/toggle]
Exercício 8: O ângulo do vértice de um triângulo isósceles mede 67° 32′ 52”. Calcule as medidas dos ângulos adjacentes à base desse triângulo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
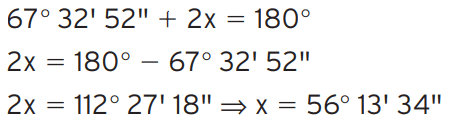
[/toggle]
Exercício 9: Calcule os valores de x e y em cada uma das figuras abaixo.
a)
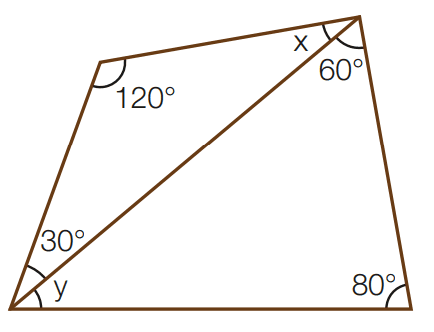
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
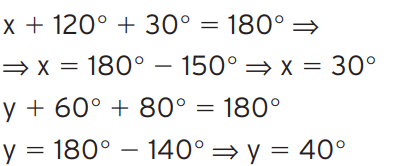
[/toggle]
b)
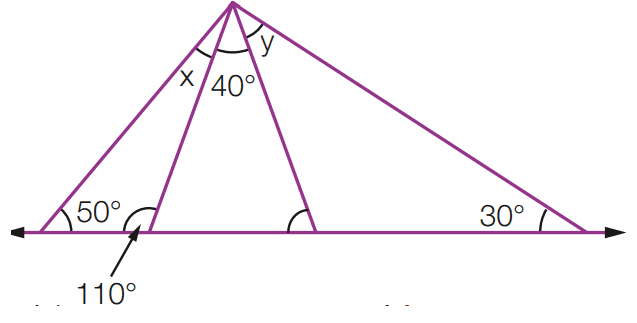
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 10: Sabendo que as retas r e s são paralelas, calcule os valores de x, y e z.
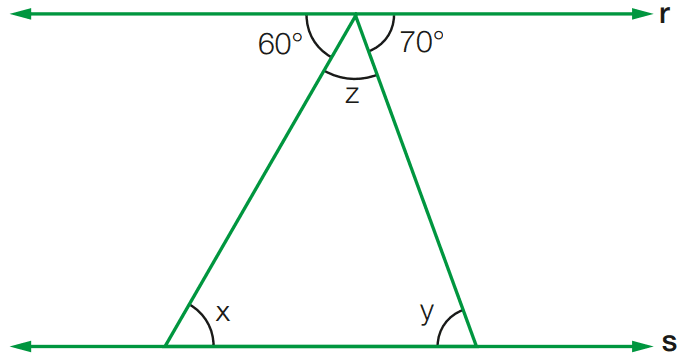
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
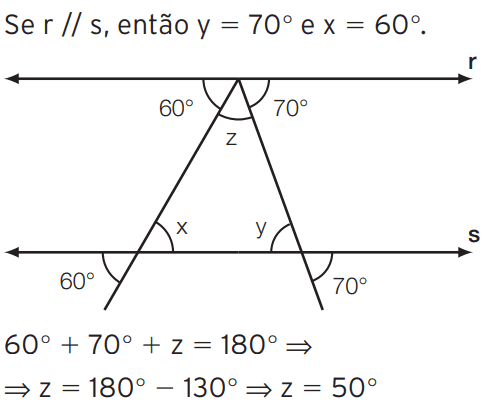
[/toggle]
Exercício 11: Sabendo que r // s, calcule o valor de x.
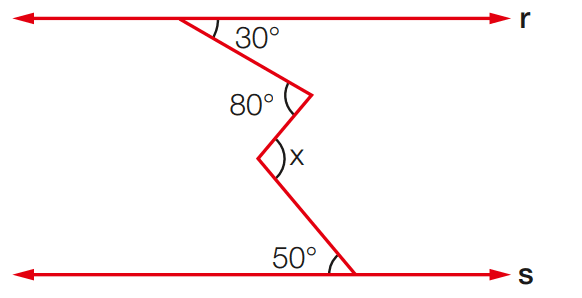
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
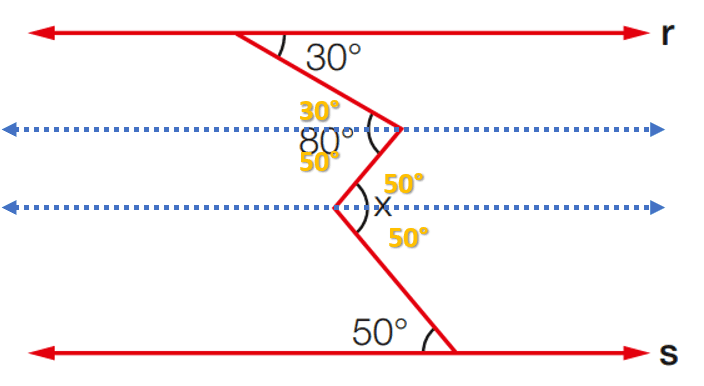
x = 50 + 50
x = 100
[/toggle]
Exercício 12: Sabendo que r // s, calcule os valores de x e y.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 13: Determine o valor de x em cada caso.
a)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x = 130 + 40 ⇨ x = 170
[/toggle]
b)

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 150 = 30
x = 90 + 30 ⇨ x = 120
[/toggle]
c)
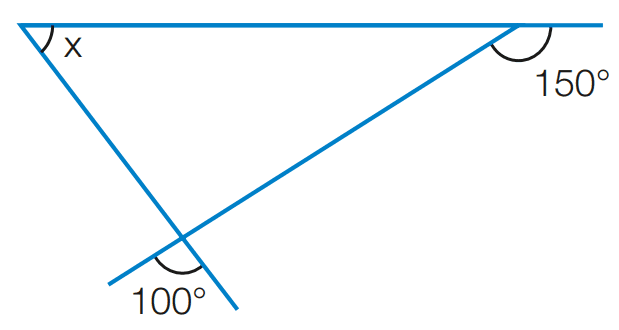
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 150 = 30
x + 100 + 30 = 180
x = 180 – 100 – 30
x = 50
[/toggle]
d)
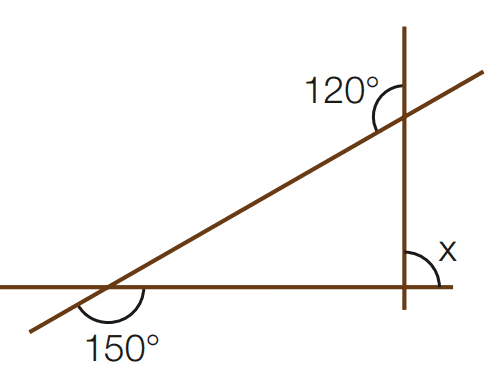
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 120 = 60
180 – 150 = 30
x = 30 + 60 ⇨ x = 90
[/toggle]
e)
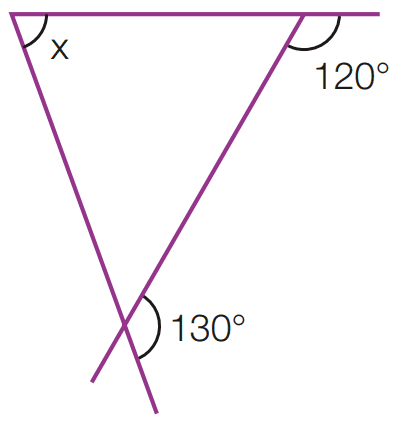
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 120 = 60
180 – 130 = 50
x + 60 + 50 = 180
x = 180 – 110
x = 70
[/toggle]
Exercício 14: Determine a medida dos ângulos internos de um triângulo, sabendo que os ângulos externos medem, em graus, respectivamente: x, x + 10 e x – 10
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
x + x + 10 + x – 10 = 180
3x = 180
x = 180/3
x = 60
1) x + 10 = 60 + 10 = 70
2) x – 10 = 60 – 10 = 50
3) x = 60
[/toggle]
Exercício 15: Calcule o valor de x na figura abaixo.
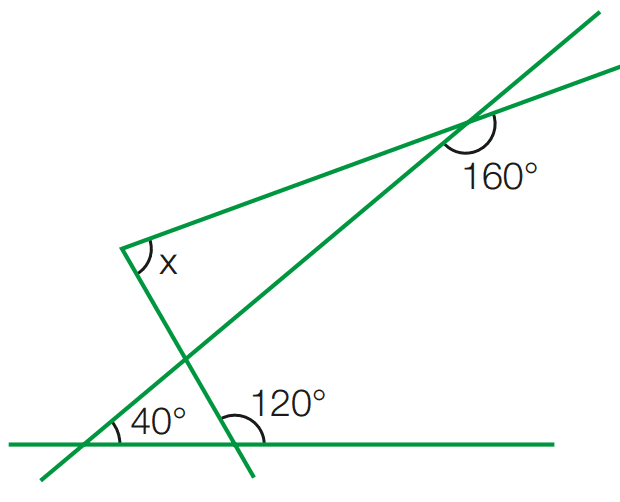
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
180 – 160 = 40
180 – 120 = 60
y + 40 + 60 = 180
y = 180 – 100
y = 80 (ângulo opv)
x + 20 + 80 = 180
x = 180 – 100
x = 80
[/toggle]
A geometria é uma área fundamental da matemática, dedicada ao estudo das formas, tamanhos e propriedades de figuras no plano e no espaço.
Leia também…