Matemática • Funções & Exponenciais • Logaritmos
Logaritmos — guia completo com propriedades, mudança de base e exercícios
Definição formal, condições de existência, propriedades, mudança de base, exemplos resolvidos e uma lista de exercícios com gabarito passo a passo. Ideal para ENEM, vestibulares e concursos.
O que é um logaritmo?
O logaritmo de um número positivo \(a\) na base \(b\) (com \(b>0\) e \(b\neq 1\)) é o expoente \(x\) tal que \(b^x=a\):
\[
\log_b a = x \;\Longleftrightarrow\; b^x = a
\]
Exemplo: \(\log_2 8=3\), pois \(2^3=8\).
Em calculadoras/planilhas, log normalmente é base 10 e ln é base \(e\) (natural).
Condições de existência
- Logaritmando: \(a > 0\).
- Base: \(b > 0\) e \(b \neq 1\).
Antes de resolver equações logarítmicas, verifique o domínio (o que está dentro do log deve ser positivo).
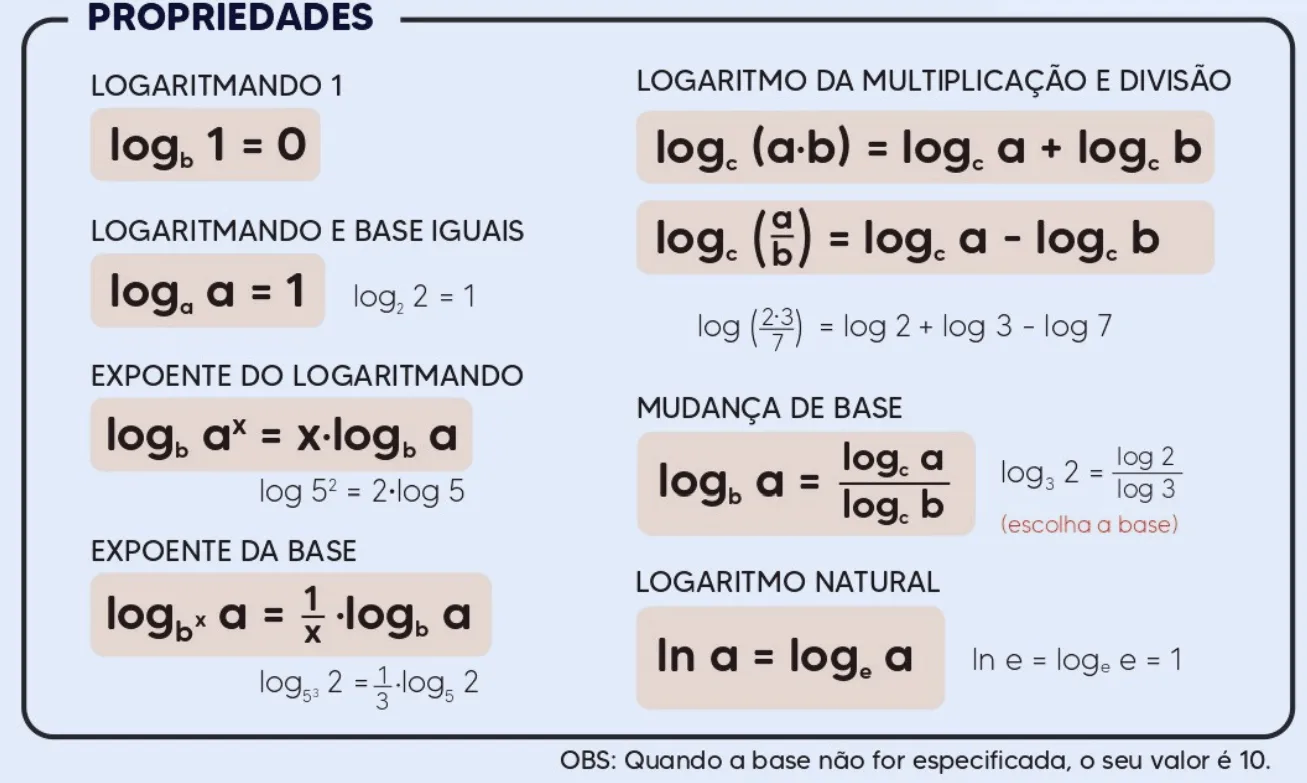
Propriedades fundamentais
1) Produto
\(\displaystyle \log_b(MN)=\log_b M+\log_b N\)
\(\log_2(4\cdot 8)=\log_2 4+\log_2 8=2+3=5\).
2) Quociente
\(\displaystyle \log_b\!\left(\frac{M}{N}\right)=\log_b M-\log_b N\)
\(\log_3\!\left(\frac{81}{9}\right)=4-2=2\).
3) Potência
\(\displaystyle \log_b(M^k)=k\cdot \log_b M\)
\(\log_5(25^3)=3\cdot \log_5 25=3\cdot 2=6\).
4) Logaritmo de 1 e da base
\(\log_b 1=0 \quad\text{e}\quad \log_b b=1\).
5) Troca entre logaritmos de bases diferentes
\(\displaystyle \log_b a=\frac{1}{\log_a b}\)
\(\log_2 8=\frac{1}{\log_8 2}=\frac{1}{1/3}=3\).
Mudança de base
\[
\log_b a=\frac{\log_k a}{\log_k b}\qquad (k>0,\;k\neq 1)
\]
\(\displaystyle \log_2 100=\frac{\log_{10}100}{\log_{10}2}=\frac{2}{0,3010}\approx 6{,}64.\)
Exemplos resolvidos
Exemplo 1. Resolver \(\log_3(x-1)=4\).
Forma exponencial: \(x-1=3^4=81\Rightarrow x=82\).
Forma exponencial: \(x-1=3^4=81\Rightarrow x=82\).
Resposta: x = 82 ✅
Exemplo 2. Resolver \(\log_2(x+4)=5\).
\(x+4=2^5=32\Rightarrow x=28\).
\(x+4=2^5=32\Rightarrow x=28\).
Resposta: x = 28 ✅
Exemplo 3. Simplificar \(\log_5(125\sqrt{5})\).
\(\log_5(125)+\log_5(\sqrt{5})=3+\tfrac12=3{,}5\).
\(\log_5(125)+\log_5(\sqrt{5})=3+\tfrac12=3{,}5\).
Resultado: 3,5 ✅
Exemplo 4. Resolver \(\log_{10}(2x-6)=\log_{10}(x)\).
Domínio: \(x>0\) e \(2x-6>0\Rightarrow x>3\). Igualando: \(2x-6=x\Rightarrow x=6\).
Domínio: \(x>0\) e \(2x-6>0\Rightarrow x>3\). Igualando: \(2x-6=x\Rightarrow x=6\).
Resposta: x = 6 (válido no domínio) ✅
Exercícios propostos (com solução em toggle)
📌 Ex. 1 — Calcule \(\log_2(32)\cdot \log_4(16)\)
\(\log_2(32)=5\) e \(\log_4(16)=\frac{\log_2 16}{\log_2 4}=\frac{4}{2}=2\).
Produto: \(5\cdot 2=10\).
Produto: \(5\cdot 2=10\).
Gabarito: 10
📌 Ex. 2 — Resolva \(\log_3(x+6)=2\)
\(x+6=3^2=9\Rightarrow x=3\). Domínio: \(x>-6\).
Gabarito: x = 3
📌 Ex. 3 — Simplifique \(\log_a\!\left(\dfrac{a^7}{\sqrt{a}}\right)\) (com \(a>0\), \(a\neq 1\))
\(\log_a(a^7)-\log_a(a^{1/2})=7-\tfrac12=6{,}5\).
Gabarito: 6,5
📌 Ex. 4 — Encontre \(x\) em \(\log_5(3x-1)=\log_5(2x+4)\)
\(3x-1=2x+4\Rightarrow x=5\). Domínio: \(x>\tfrac13\) e \(x>-2\) — válido.
Gabarito: x = 5
📌 Ex. 5 — Use mudança de base para \(\log_2(50)\) (base 10)
\(\displaystyle \log_2(50)=\frac{\log 50}{\log 2}\approx \frac{1{,}6990}{0{,}3010}\approx 5{,}64.\)
Gabarito: ≈ 5,64
📌 Ex. 6 — Resolva \(\log_{1/2}(x)=3\)
Base \(1/2\in(0,1)\). Forma exponencial: \(\left(\tfrac12\right)^3=x \Rightarrow x=\tfrac{1}{8}\).
Gabarito: \(x=\tfrac{1}{8}\)
📌 Ex. 7 — Simplifique \(\log_3(27\sqrt{3})\)
\(\log_3 27 + \log_3 \sqrt{3}=3+\tfrac12=3{,}5\).
Gabarito: 3,5
📌 Ex. 8 — Resolva \(\log_4(x-4)+\log_4(x)=2\)
Produto: \(\log_4\big(x(x-4)\big)=2 \Rightarrow x(x-4)=4^2=16\).
\(x^2-4x-16=0\Rightarrow x=\frac{4\pm\sqrt{16+64}}{2}=2\pm 2\sqrt{5}\).
Domínio: \(x>4\) para \(x-4>0\). Logo, \(x=2+2\sqrt{5}\approx 6{,}472\).
\(x^2-4x-16=0\Rightarrow x=\frac{4\pm\sqrt{16+64}}{2}=2\pm 2\sqrt{5}\).
Domínio: \(x>4\) para \(x-4>0\). Logo, \(x=2+2\sqrt{5}\approx 6{,}472\).
Gabarito: \(x=2+2\sqrt{5}\)
📌 Ex. 9 — Calcule \(\dfrac{\log_5 20}{\log_5 2}\)
Mudança de base relativa: \(\dfrac{\log_5 20}{\log_5 2}=\log_2 20\).
\(\log_2 20=\log_2(4\cdot5)=\log_2 4+\log_2 5=2+\log_2 5\approx 2+2{,}322=4{,}322\).
\(\log_2 20=\log_2(4\cdot5)=\log_2 4+\log_2 5=2+\log_2 5\approx 2+2{,}322=4{,}322\).
Gabarito: ≈ 4,322
📌 Ex. 10 — Resolva \(\log_{10}(x^2-9)=1\)
\(x^2-9=10^1=10 \Rightarrow x^2=19 \Rightarrow x=\pm \sqrt{19}\).
Domínio: \(x^2-9>0\) — ambos os valores servem.
Domínio: \(x^2-9>0\) — ambos os valores servem.
Gabarito: \(x=\pm\sqrt{19}\)
Aplicações dos logaritmos
- Escalas científicas: Richter (terremotos) e decibéis (som) são logarítmicas.
- Crescimento/decadência: modelos exponenciais em biologia, química e finanças.
- Algoritmos: complexidade \(O(\log n)\) em busca binária e árvores balanceadas.
Aprofunde em Funções Exponenciais e
Equações Exponenciais.
Próximos passos e linkagem interna (SEO)
Conjuntos Numéricos
Naturais, Inteiros, Racionais, Irracionais e Reais.
Números Reais
Base para domínios de funções e logaritmos.
Operações com Reais
Algebra útil para manipular logs.
Banco de Questões
Pratique por assunto e dificuldade.
Artigo otimizado para leitura no celular (blocos verticais, fórmulas centralizadas). Bons estudos! 👊















