Confira questões resolvidas de Matemática da banca IBFC, organizadas e explicadas passo a passo. Ideal para quem busca praticar e entender os padrões dessa banca em concursos. Aperfeiçoe seus estudos com questões de matemática IBFC e melhore seu desempenho!
👉Livro Indicado Matemática para Concurso
(IBFC – 2023 – Trigonometria) Considere M, N e P conjuntos de números reais. Sejam f : M → N e g: N → P funções definidas, respectivamente, por 𝒇(𝒙) = 𝒔𝒆𝒏(𝒙), x ∈ M e 𝒈(𝒙) = 𝟏/(𝟏−𝟐𝒙𝟐). Existe uma função h: M → P, definida por 𝒉(𝒙) = 𝒈(𝒇(𝒙)), tal que:
A) h(x) = sec(2x)
B) h(x) = −sen(2x)
C) h(x) = cossec(2x)
D) h(x) = cos(2x)
E) h(x) = tg(2x)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Para resolver essa questão, vamos determinar a função h(x) definida por h(x) = g(f(x)).
Dado:
- f(x) = sin(x)
- g(x) = 1/(1 – 2x2)
A função h(x) é dada por:
h(x) = g(f(x))
Passo 1: Substituir f(x) em g(x)
Como f(x) = sin(x), substituímos sin(x) em g(x):
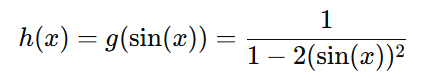
Passo 2: Simplificar h(x) usando identidades trigonométricas
Sabemos da identidade trigonométrica:
cos(2x) = 1 – 2sin2(x)
Portanto, podemos substituir 1 – 2sin2(x) por cos(2x):
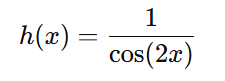
A função h(x) é então:
h(x) = sec(2x)
Resposta
Alternativa correta: A) ( h(x) = sec(2x)
Gostou da explicação? Continue praticando com mais questões matemática IBFC, e confira um Livro de Matemática indicado.
[/toggle]
🟣Questões de Matemática IBFC (Nível Fundamental) – PDF Exclusivo para Concursos
🟠Questões de Matemática IBFC (Nível Médio) – PDF Exclusivo para Concursos
🔴Questões de Matemática IBFC (Nível Superior) – PDF Exclusivo para Concursos
🟢Mapas Mentais de Matemática para Concurso

























