Uma mola é solta da posição distendida conforme a figura. A figura à direita representa o gráfico da posição \(P\) (em cm) da massa \(m\) em função do tempo \(t\) (em segundo) em um sistema de coordenadas cartesianas.
Esse movimento periódico é descrito por uma expressão do tipo \(P(t)=\pm A\cos(\omega t)\) ou \(P(t)=\pm A\sin(\omega t)\), em que \(A>0\) é a amplitude de deslocamento máximo e \(\omega\) é a frequência, que se relaciona com o período \(T\) pela fórmula \(\omega=\dfrac{2\pi}{T}\). Considere a ausência de quaisquer forças dissipativas.
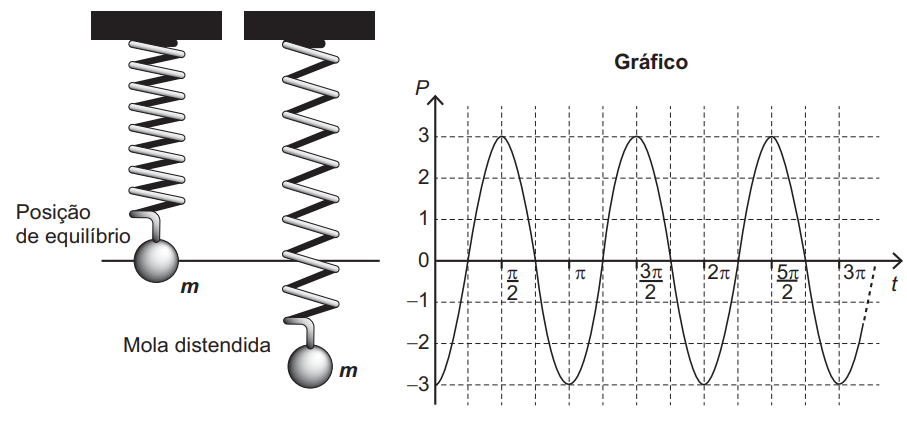
A expressão algébrica que representa as posições \(P(t)\) da massa \(m\), ao longo do tempo, no gráfico, é
- \(-3\cos(2t)\)
- \(-3\sin(2t)\)
- \(3\cos(2t)\)
- \(-6\cos(2t)\)
- \(6\sin(2t)\)
Mostrar / esconder solução passo a passo
1) Período e frequência
Pelo gráfico, o período é \(T=\pi\). Logo \[ \omega=\frac{2\pi}{T}=\frac{2\pi}{\pi}=2. \]
Pelo gráfico, o período é \(T=\pi\). Logo \[ \omega=\frac{2\pi}{T}=\frac{2\pi}{\pi}=2. \]
2) Amplitude e fase inicial
Observando o eixo vertical, \(|P|\le 3\) ⇒ \(A=3\).
Em \(t=0\) o gráfico está no valor mínimo, \(P(0)=-3\).
Para \(\cos\), temos \(\cos(0)=1\); para obter \(-3\) em \(t=0\), \[ P(0)= -3\cos(0) = -3. \] Assim, a forma compatível é \(P(t)=-3\cos(\omega t)\).
Observando o eixo vertical, \(|P|\le 3\) ⇒ \(A=3\).
Em \(t=0\) o gráfico está no valor mínimo, \(P(0)=-3\).
Para \(\cos\), temos \(\cos(0)=1\); para obter \(-3\) em \(t=0\), \[ P(0)= -3\cos(0) = -3. \] Assim, a forma compatível é \(P(t)=-3\cos(\omega t)\).
3) Função final
Substituindo \(\omega=2\): \[ \boxed{P(t)=-3\cos(2t)}. \] Gabarito: Alternativa A.
Substituindo \(\omega=2\): \[ \boxed{P(t)=-3\cos(2t)}. \] Gabarito: Alternativa A.
Página desta questão:
ENEM 2021 — Matemática — Questão 25 — Movimento harmônico (mola)
.
Mais questões ENEM Matemática: acessar.
Mapas Mentais: ver.
10 eBooks de Matemática: baixar.













