Questão 20
Um proprietário pretende instalar um sensor de presença para a proteção de seu imóvel. O sensor deverá detectar movimentos de objetos e pessoas numa determinada região plana. A figura ilustra a vista superior da área de cobertura (setor circular em azul) de um sensor colocado no ponto S. Essa área depende da medida do ângulo \( \alpha \), em grau, e do raio \( R \), em metro.
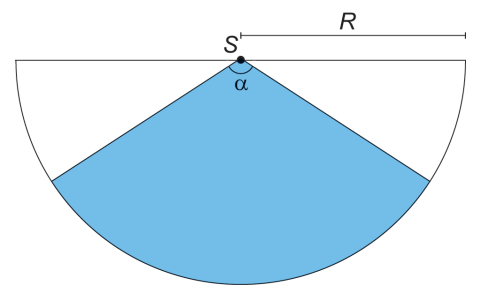
Ao aumentar o ângulo \( \alpha \) ou o raio \( R \) aumenta-se a área de cobertura do sensor. Entretanto, quanto maior essa área, maior o preço do sensor.
Para esse fim, há cinco tipos de sensores disponíveis no mercado, cada um com as seguintes características:
- Tipo I: \( \alpha = 15^\circ \) e \( R = 20 \, \text{m} \);
- Tipo II: \( \alpha = 30^\circ \) e \( R = 22 \, \text{m} \);
- Tipo III: \( \alpha = 40^\circ \) e \( R = 12 \, \text{m} \);
- Tipo IV: \( \alpha = 60^\circ \) e \( R = 16 \, \text{m} \);
- Tipo V: \( \alpha = 90^\circ \) e \( R = 10 \, \text{m} \).
Esse proprietário pretende adquirir um desses sensores que seja capaz de cobrir, no mínimo, uma área de medida 70 \( \text{m}^2 \), com o menor preço possível.
Use 3 como valor aproximado para \( \pi \).
O proprietário do imóvel deverá adquirir o sensor do tipo:
- A) I
- B) II
- C) III
- D) IV
- E) V
Ver Solução
Fórmula da área do setor circular:
\[ A = \frac{\alpha}{360} \cdot \pi R^2 \]
Use \( \pi \approx 3 \)
—Tipo I:
\[ A = \frac{15}{360} \cdot 3 \cdot 20^2 = \frac{1}{24} \cdot 3 \cdot 400 = 50 \, \text{m}^2 \]
Tipo II:
\[ A = \frac{30}{360} \cdot 3 \cdot 22^2 = \frac{1}{12} \cdot 3 \cdot 484 = \frac{1452}{12} = 121 \, \text{m}^2 \]
Tipo III:
\[ A = \frac{40}{360} \cdot 3 \cdot 12^2 = \frac{1}{9} \cdot 3 \cdot 144 = 48 \, \text{m}^2 \]
Tipo IV:
\[ A = \frac{60}{360} \cdot 3 \cdot 16^2 = \frac{1}{6} \cdot 3 \cdot 256 = 128 \, \text{m}^2 \]
Tipo V:
\[ A = \frac{90}{360} \cdot 3 \cdot 10^2 = \frac{1}{4} \cdot 3 \cdot 100 = 75 \, \text{m}^2 \]
—Sensores que atendem: II, IV, V
Menor área possível ≥ 70 m²: Tipo V → 75 m²
Logo, o menor custo possível para atender a necessidade é com o sensor do tipo: V
Resposta correta: alternativa E













