Questão 37
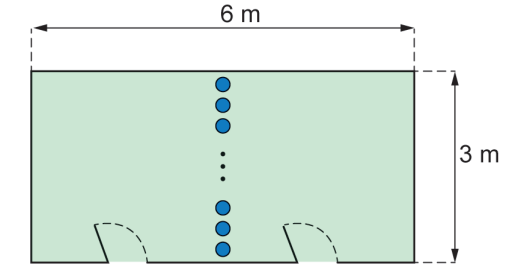
Uma sala com piso no formato retangular, com lados de medidas 3 m e 6 m, será dividida em dois ambientes. Para isso, serão utilizadas colunas em formato cilíndrico, dispostas perpendicularmente ao piso e representadas na figura pelos círculos de cor azul. Os centros desses círculos estarão sobre uma reta paralela aos lados de menor medida do piso da sala. Os vãos entre duas colunas e entre uma coluna e a parede não poderão ser superiores a 15 cm.
Para efetuar a compra dessas colunas, foram feitos orçamentos com base em dados fornecidos por cinco lojas:
| Loja | Raio (cm) | Preço por unidade (R$) |
|---|---|---|
| I | 5 | 60 |
| II | 10 | 70 |
| III | 12 | 75 |
| IV | 15 | 90 |
| V | 20 | 120 |
A compra será realizada na loja cujo orçamento resulte no menor valor total possível.
- A) I
- B) II
- C) III
- D) IV
- E) V
1. Análise geométrica:
As colunas devem ser colocadas ao longo do lado de 6 m (600 cm), com distância máxima de 15 cm entre elas e as paredes.
Sejam \( r \) o raio da coluna e \( d = 2r \) o diâmetro. A distância entre os centros das colunas será: \[ \text{espaço útil} = 600 – 2r \quad (\text{subtrai-se a margem de } r \text{ em cada lado}) \]
Número de vãos = \( n – 1 \), onde \( n \) é o número de colunas.
Distância entre colunas: \( \frac{600 – 2r}{n – 1} \leq 15 \)
Aplicando isso para cada loja:
- Loja I (r = 5): \( \frac{600 – 10}{15} = 39,3 \Rightarrow n = 41 \Rightarrow 41 × 60 = R$ 2.460 \)
- Loja II (r = 10): \( \frac{600 – 20}{15} = 38.6 \Rightarrow n = 40 \Rightarrow 40 × 70 = R$ 2.800 \)
- Loja III (r = 12): \( \frac{600 – 24}{15} = 38.4 \Rightarrow n = 39 \Rightarrow 39 × 75 = R$ 2.925
- Loja IV (r = 15): \( \frac{600 – 30}{15} = 38 \Rightarrow n = 39 \Rightarrow 39 × 90 = R$ 3.510
- Loja V (r = 20): \( \frac{600 – 40}{15} = 37.3 \Rightarrow n = 38 \Rightarrow 38 × 120 = R$ 4.560
Menor valor: Loja III → R$ 2.925
Resposta correta: alternativa C
[/toggle]












