Questão 13
Um aeroporto disponibiliza o serviço de transporte gratuito entre seus dois terminais utilizando os ônibus A e B, que partem simultaneamente, de hora em hora, de terminais diferentes.
A distância entre os terminais é de 9000 metros, e o percurso total dos ônibus, de um terminal ao outro, é monitorado por um sistema de cinco câmeras que cobrem diferentes partes do trecho, conforme o esquema:
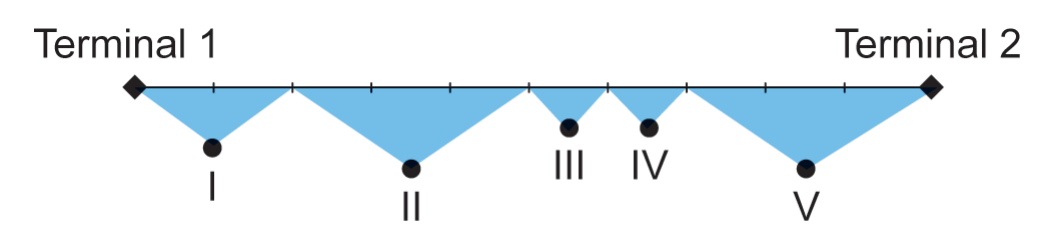
O alcance de cada uma das cinco câmeras é:
- câmera I: \( \frac{1}{5} \) do percurso
- câmera II: \( \frac{3}{10} \) do percurso
- câmera III: \( \frac{1}{10} \) do percurso
- câmera IV: \( \frac{1}{10} \) do percurso
- câmera V: \( \frac{3}{10} \) do percurso
No mesmo instante:
- Ônibus A parte do Terminal 1 a 250 m/min
- Ônibus B parte do Terminal 2 a 150 m/min
Qual câmera registra o momento em que os ônibus A e B se encontram?
- A) I
- B) II
- C) III
- D) IV
- E) V
1. Distância total entre os terminais: \( 9000 \, \text{m} \)
Os ônibus partem de lados opostos e caminham um em direção ao outro. Quando se encontram, a soma das distâncias percorridas por ambos será 9000 metros.
—2. Velocidades:
- A: 250 m/min
- B: 150 m/min
Soma das velocidades: \( 250 + 150 = 400 \, \text{m/min} \)
Tempo até o encontro:
\[ t = \frac{9000}{400} = 22{,}5 \, \text{min} \]
—3. Distância que cada um percorre nesse tempo:
- A: \( 250 \cdot 22{,}5 = 5625 \, \text{m} \)
- B: \( 150 \cdot 22{,}5 = 3375 \, \text{m} \)
4. Qual câmera cobre a posição 5625 m a partir do Terminal 1?
Vamos dividir o percurso com base nas frações indicadas:
- Câmera I: até \( \frac{1}{5} \cdot 9000 = 1800 \, \text{m} \)
- Câmera II: \( 1800 \) até \( 1800 + \frac{3}{10} \cdot 9000 = 1800 + 2700 = 4500 \, \text{m} \)
- Câmera III: \( 4500 \) até \( 4500 + 900 = 5400 \, \text{m} \)
- Câmera IV: \( 5400 \) até \( 5400 + 900 = 6300 \, \text{m} \)
- Câmera V: \( 6300 \) até 9000 m
Como 5625 m está entre 5400 m e 6300 m, o encontro acontece sob a Câmera IV.
Resposta correta: alternativa D
[/toggle]












