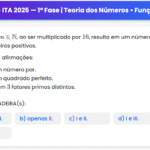
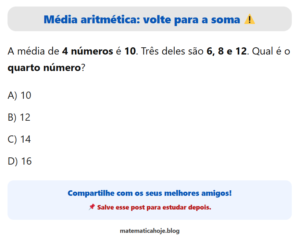
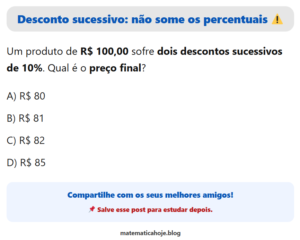
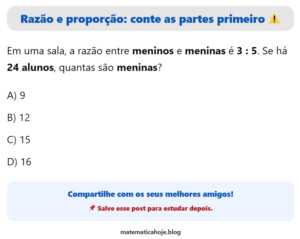
ITA 2020 — 2ª Fase — Questão 5 — Números Complexos
Seja \(z\in\mathbb{C}\) uma raiz da equação
\[
4z^2-4z\sin\alpha+1=0,\qquad \alpha\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right].
\]
Determine, em função de \(\alpha\), todos os possíveis valores de:
a) \(\displaystyle 2z+\frac{1}{2z}\).
b) \(\displaystyle (2z)^{15}+\frac{1}{(2z)^{15}}\).
b) \(\displaystyle (2z)^{15}+\frac{1}{(2z)^{15}}\).
👀 Solução detalhada
Passo 1 — Escreva \(2z\) em forma trigonométrica.
Da quadrática \(4z^2-4z\sin\alpha+1=0\), o discriminante é \(\Delta=16\sin^2\alpha-16=-16\cos^2\alpha\le0\). Assim, \[ 2z=\sin\alpha\ \pm\ i\cos\alpha. \] Note que \(|2z|=1\), logo \(\displaystyle \frac{1}{2z}=\overline{2z}=\sin\alpha\mp i\cos\alpha\).
a) Cálculo de \(2z+\dfrac{1}{2z}\)
Somando os conjugados: \[ 2z+\frac{1}{2z}=(\sin\alpha+i\cos\alpha)+(\sin\alpha-i\cos\alpha)=2\sin\alpha. \] Portanto, independe da escolha do sinal: \[ \boxed{\,2z+\dfrac{1}{2z}=2\sin\alpha\, }. \]
b) Cálculo de \((2z)^{15}+\dfrac{1}{(2z)^{15}}\)
Tome \(2z_1=\sin\alpha+i\cos\alpha\). Observe que \[ \sin\alpha+i\cos\alpha=\cos\!\left(\tfrac{\pi}{2}-\alpha\right)+ i\sin\!\left(\tfrac{\pi}{2}-\alpha\right)=\operatorname{cis}\!\left(\tfrac{\pi}{2}-\alpha\right). \] Pelo Teorema de De Moivre, \[ (2z_1)^{15}=\operatorname{cis}\!\left(15\Big(\tfrac{\pi}{2}-\alpha\Big)\right),\qquad \frac{1}{(2z_1)^{15}}=\operatorname{cis}\!\left(-15\Big(\tfrac{\pi}{2}-\alpha\Big)\right). \] Logo, \[ (2z_1)^{15}+\frac{1}{(2z_1)^{15}} =2\cos\!\left(15\Big(\tfrac{\pi}{2}-\alpha\Big)\right) =2\cos\!\left(\tfrac{15\pi}{2}-15\alpha\right). \] Como \(\cos\!\left(\tfrac{15\pi}{2}-x\right)=\cos\!\left(7\pi+\tfrac{\pi}{2}-x\right) =-\sin x\), obtemos \[ (2z_1)^{15}+\frac{1}{(2z_1)^{15}}=-2\sin(15\alpha). \] Se tomarmos a outra raiz \(2z_2=\sin\alpha-i\cos\alpha=\operatorname{cis}\!\left(-\tfrac{\pi}{2}+\alpha\right)\), o mesmo raciocínio leva ao mesmo valor. Assim, o resultado é único: \[ \boxed{\, (2z)^{15}+\dfrac{1}{(2z)^{15}}=-2\sin(15\alpha)\, }. \]
Da quadrática \(4z^2-4z\sin\alpha+1=0\), o discriminante é \(\Delta=16\sin^2\alpha-16=-16\cos^2\alpha\le0\). Assim, \[ 2z=\sin\alpha\ \pm\ i\cos\alpha. \] Note que \(|2z|=1\), logo \(\displaystyle \frac{1}{2z}=\overline{2z}=\sin\alpha\mp i\cos\alpha\).
a) Cálculo de \(2z+\dfrac{1}{2z}\)
Somando os conjugados: \[ 2z+\frac{1}{2z}=(\sin\alpha+i\cos\alpha)+(\sin\alpha-i\cos\alpha)=2\sin\alpha. \] Portanto, independe da escolha do sinal: \[ \boxed{\,2z+\dfrac{1}{2z}=2\sin\alpha\, }. \]
b) Cálculo de \((2z)^{15}+\dfrac{1}{(2z)^{15}}\)
Tome \(2z_1=\sin\alpha+i\cos\alpha\). Observe que \[ \sin\alpha+i\cos\alpha=\cos\!\left(\tfrac{\pi}{2}-\alpha\right)+ i\sin\!\left(\tfrac{\pi}{2}-\alpha\right)=\operatorname{cis}\!\left(\tfrac{\pi}{2}-\alpha\right). \] Pelo Teorema de De Moivre, \[ (2z_1)^{15}=\operatorname{cis}\!\left(15\Big(\tfrac{\pi}{2}-\alpha\Big)\right),\qquad \frac{1}{(2z_1)^{15}}=\operatorname{cis}\!\left(-15\Big(\tfrac{\pi}{2}-\alpha\Big)\right). \] Logo, \[ (2z_1)^{15}+\frac{1}{(2z_1)^{15}} =2\cos\!\left(15\Big(\tfrac{\pi}{2}-\alpha\Big)\right) =2\cos\!\left(\tfrac{15\pi}{2}-15\alpha\right). \] Como \(\cos\!\left(\tfrac{15\pi}{2}-x\right)=\cos\!\left(7\pi+\tfrac{\pi}{2}-x\right) =-\sin x\), obtemos \[ (2z_1)^{15}+\frac{1}{(2z_1)^{15}}=-2\sin(15\alpha). \] Se tomarmos a outra raiz \(2z_2=\sin\alpha-i\cos\alpha=\operatorname{cis}\!\left(-\tfrac{\pi}{2}+\alpha\right)\), o mesmo raciocínio leva ao mesmo valor. Assim, o resultado é único: \[ \boxed{\, (2z)^{15}+\dfrac{1}{(2z)^{15}}=-2\sin(15\alpha)\, }. \]
Resumo: a) \(2\sin\alpha\). b) \(-2\sin(15\alpha)\).
🔗 Veja também a questão anterior:
Matemática ITA 2020 — Questão 4 — 2ª Fase