Os quatro indicadores mais importantes da estatística descritiva aparecem em provas, concursos, Enem, exames de escolas e também em situações práticas do dia a dia. Média, moda, mediana e amplitude ajudam a entender rapidamente um conjunto numérico, revelando padrões, tendências e comportamentos dos dados. Neste artigo, você vai aprender a interpretar cada medida de forma simples, com explicações claras, exemplos resolvidos e uma lista de exercícios com soluções passo a passo.
Logo abaixo está uma imagem-resumo produzida especialmente para facilitar seus estudos.
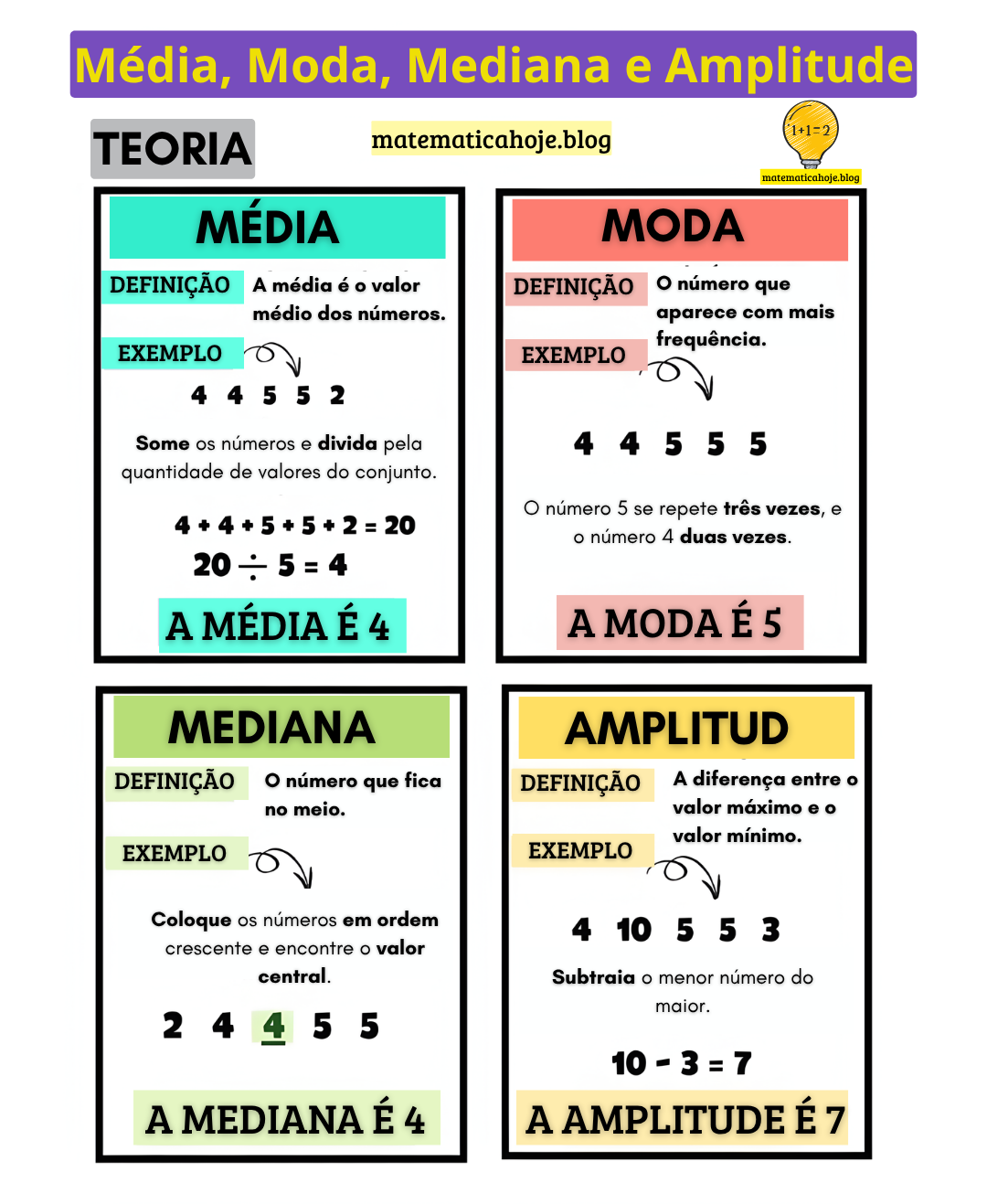
O que significa média e como utilizá-la corretamente
A média aritmética é provavelmente a medida estatística mais famosa. Ela representa o “valor típico” de um conjunto de números. Para calcular, some todos os valores e divida pela quantidade de elementos.
Exemplo prático de cálculo da média
Conjunto: 4, 5, 5, 4, 2
Somando:
$4 + 5 + 5 + 4 + 2 = 20$
Dividindo pela quantidade de valores (5):
$20 ÷ 5 = 4$
✅ A média é igual a 4.
Moda: o número que mais se repete no conjunto
Moda é a medida que representa o valor mais frequente. Alguns conjuntos podem ter uma moda, várias modas ou nenhuma moda.
Exemplo prático
Conjunto: 4, 4, 5, 5, 5
O número 5 aparece 3 vezes. Logo: ✅ A moda é 5.
Mediana: o valor que ocupa a posição central
A mediana é o número que fica exatamente no meio após ordenar os dados. Se o conjunto tiver quantidade ímpar de valores, basta pegar o valor central. Se for par, calcula-se a média dos dois números centrais.
Exemplo prático
Conjunto: 2, 4, 4, 5, 5
Valor central → 4
✅ A mediana é 4.
Amplitude: diferença entre o maior e o menor valor
A amplitude mostra o quanto os dados variam. Para calcular, basta subtrair o menor número do maior.
Exemplo prático
Conjunto: 4, 10, 5, 5, 3
Maior valor: 10 Menor valor: 3
$10 – 3 = 7$
✅ A amplitude é 7.
Lista de exercícios resolvidos (com botão abre/fecha)
Questão 1 — Média e Amplitude
Os valores 6, 8, 10, 4 e 12 representam a produção diária de uma máquina. Calcule a média e a amplitude desses dados.
Média:
$6 + 8 + 10 + 4 + 12 = 40$
$40 ÷ 5 = 8$
Amplitude:
Maior valor: 12
Menor valor: 4
$12 – 4 = 8$
✅ Resposta: média = 8, amplitude = 8
Questão 2 — Moda e Mediana
Considere os valores 7, 9, 9, 10, 11, 12, 12. Determine a moda e a mediana.
Moda:
Os valores que se repetem são 9 e 12.
✅ Moda = 9 e 12 (bimodal)
Mediana:
Valores em ordem:
7, 9, 9, 10, 11, 12, 12
✅ Mediana = 10
Questão 3 — Conjunto real aplicado
A nota de cinco alunos foi: 5.5, 7.0, 8.0, 6.5 e 9.0. Calcule a média e determine se existe moda.
Média:
$5.5 + 7.0 + 8.0 + 6.5 + 9.0 = 36$
$36 ÷ 5 = 7.2$
Moda: nenhum valor se repete.
✅ Média = 7.2 e não existe moda.
Conclusão
Agora você aprendeu de forma didática como calcular média, moda, mediana e amplitude, além de entender quando usar cada medida e como interpretar os dados. Essas ferramentas são fundamentais em provas, estatísticas de sala de aula, análises de desempenho e até em situações simples como comparar preços e avaliar resultados.
FAQ
Para que servem média, moda e mediana no dia a dia?
Essas medidas ajudam a interpretar dados rapidamente. São usadas para analisar notas, preços, resultados de desempenho, médias de consumo, estatísticas esportivas e muito mais.
Qual é a diferença entre média e mediana?
A média considera todos os valores somados e divididos pela quantidade de dados. Já a mediana é o valor central após ordenar os números, sendo menos afetada por valores muito altos ou muito baixos.
Quando a moda é mais importante?
A moda é mais útil quando queremos identificar o valor mais frequente, como em pesquisas, fluxo de vendas, preferências de usuários ou padrões de comportamento.
Autor: Adriano Rocha






















