Os números complexos são uma extensão dos números reais que permitem a solução de equações que não possuem solução no conjunto dos números reais, como por exemplo (x2 + 1 = 0). Este conceito é fundamental em várias áreas da matemática e suas aplicações se estendem à física, engenharia elétrica, e mais. Neste artigo, vamos explorar o que são números complexos, suas principais propriedades e como operá-los.
O que são Números Complexos?
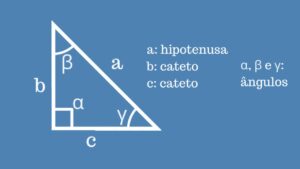
Um número complexo é formado por uma parte real e uma parte imaginária, e pode ser representado na forma:
( z = a + bi )
Onde:
- a é a parte real.
- b é a parte imaginária.
- i é a unidade imaginária, definida como √-1.
Exemplos:
- Para z = 5 + 2i, a parte real é 5 e a parte imaginária é 2i.
- Para z = -3 + 4i, a parte real é -3 e a parte imaginária é 4i.
Unidade Imaginária
A unidade imaginária i é um número com a propriedade única:
i2 = -1
A unidade imaginária obedece a um ciclo de potências:
- i3 = -i
- i4 = 1
Este ciclo se repete a cada quatro potências.
Exemplos:
- i5 = i1 = i
- i6 = i2 = -1
Conjugado de um Número Complexo
O conjugado de um número complexo z = a + bi é dado por:
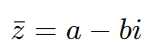
O conjugado é obtido trocando o sinal da parte imaginária. O produto de um número complexo pelo seu conjugado resulta em um número real:
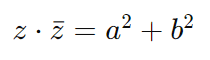
Exemplos:
- Para z = 3 + 4i, o conjugado é z¯ = 3 – 4i.
- Para z = -1 + 7i, o conjugado é z¯ = -1 – 7i.
Módulo de um Número Complexo
O módulo de um número complexo z = a + bi é a sua magnitude ou distância da origem no plano complexo, e é calculado como:

Exemplos:
- Para z = 3 + 4i, o módulo é |z| = √(32 + 42) = √5.
- Para z = 1 + i, o módulo é |z| = √(12 + 12 )= √2.
Forma Trigonométrica
Os números complexos podem ser representados na forma trigonométrica, que é útil para multiplicação e divisão de números complexos:
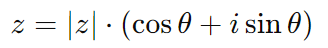
Onde θ é o argumento do número complexo, que é o ângulo formado com o eixo real.

Exemplos:
- Para z = 1 + i, com módulo |z| = √2 e θ = π/4, a forma trigonométrica é z = √2⋅(cosπ/4 + i.sin/π4)
- Para z =−1 + 3i, com módulo ∣z∣=2 e θ=2π/3, a forma trigonométrica é z = 2⋅(cos2π/3 + i.sin2/π3).
Conclusão
Os números complexos são ferramentas poderosas que ampliam o conceito dos números reais, permitindo que soluções para equações antes impossíveis possam ser encontradas. Compreender como manipular números complexos, calcular seus módulos e representar suas formas trigonométricas é essencial para o estudo avançado da matemática e suas diversas aplicações. Com esses exemplos e fórmulas destacadas, você agora tem uma base sólida para explorar mais profundamente este fascinante ramo da matemática.
Leia também
Matriz: o que é, tipos, operações, exercícios
Determinantes de Matrizes: Conceito, Exemplos e Propriedades
Sistemas Lineares Descomplicado: Guia Completo para Solução e Interpretação
Entendendo o Binômio de Newton