O que são Números Reais?

O conjunto dos números reais, representado por \(\mathbb{R}\), engloba todos os números que podem ser representados em uma reta numérica contínua:

Ele inclui os naturais, inteiros, racionais e irracionais. Para detalhes sobre parte decimal, veja também números decimais.

Subconjuntos de \(\mathbb{R}\)

• Números Naturais (\(\mathbb{N}\)): \(0,1,2,3,\dots\)
• Números Inteiros (\(\mathbb{Z}\)): \(\dots,-2,-1,0,1,2,\dots\)
• Números Racionais (\(\mathbb{Q}\)): frações e decimais periódicos
• Números Irracionais (\(\mathbb{I}\)): decimais infinitos não periódicos

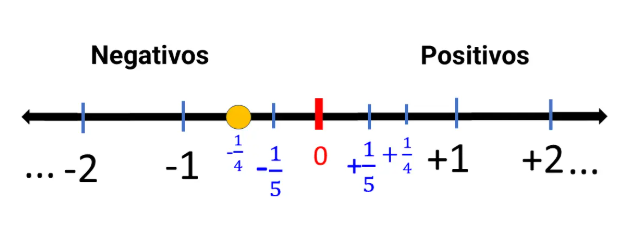
Representação na Reta Numérica

Todos os números reais têm uma posição única na reta numérica. É possível indicar frações, decimais, raízes e constantes como \(\pi\) e \(e\) diretamente na reta.

Propriedades e Operações

O conjunto \(\mathbb{R}\) é fechado para as operações básicas (+, −, ×, ÷, exceto divisão por zero) e possui estrutura de corpo ordenado:

• Comutatividade e associatividade para soma e produto
• Elemento neutro: \(0\) na soma, \(1\) no produto
• Existência de simétricos e inversos
• Distributividade: \(a(b+c)=ab+ac\)

Densidade dos Reais

O conjunto \(\mathbb{R}\) é denso: entre dois números distintos, sempre há infinitos racionais e irracionais. Isso garante que a reta numérica não tem “lacunas”.

Exemplos Resolvidos

Exemplo 1 — Classificação

Enunciado: Classifique os números: \(\sqrt{9}\), \(\pi\), \(-5\), \(\dfrac{7}{3}\).

Exemplo 2 — Intervalos

Enunciado: Escreva o intervalo de todos os números reais maiores que 2 e menores que 5.

Exercícios Propostos

1. Classifique: \(\sqrt{2}\), \(3,5\), \(-8\), \(0,\overline{6}\).
2. Represente na reta: os números \(0\), \(\pi\) e \(-2\).
3. Determine o conjunto dos números reais \(x\) tais que \(1 < x \leq 4\).
4. Mostre que entre \(1\) e \(2\) existem infinitos números racionais.

Resumo e Materiais

• ✔ Definição e subconjuntos de \(\mathbb{R}\)
• ✔ Representação na reta numérica
• ✔ Propriedades e operações
• ✔ Exemplos resolvidos e exercícios