O estudo do cálculo é uma das maiores conquistas da matemática e está diretamente ligado à nossa capacidade de compreender e prever mudanças no mundo real. Seja no crescimento de uma população, na velocidade de um carro ou no fluxo de corrente elétrica, o cálculo nos dá as ferramentas para descrever e modelar transformações.
Neste artigo, vamos explorar o que é o cálculo, como ele surgiu e qual a importância do conceito de limite, o verdadeiro alicerce do cálculo diferencial e integral.
O que é o Cálculo?
A palavra “cálculo” vem do latim calculus, que significava “pedrinha usada para contar”. Com o passar dos séculos, o termo evoluiu para representar uma das mais sofisticadas ferramentas do pensamento humano: o Cálculo Infinitesimal, que se desdobra em dois grandes ramos:
- Cálculo Diferencial: estuda variações instantâneas — como a velocidade de um objeto num ponto exato do tempo.
- Cálculo Integral: analisa a soma de infinitas pequenas partes — como o total de área sob uma curva.
Juntos, esses dois ramos permitem resolver problemas complexos de geometria, física, economia, biologia e engenharia.
Breve História do Cálculo
Apesar de sua formulação moderna ter sido feita por Isaac Newton e Gottfried Wilhelm Leibniz no século XVII, a origem do cálculo é muito mais antiga. Desde a Grécia Antiga, matemáticos como Eudóxio de Cnido e Arquimedes já utilizavam conceitos parecidos com os limites para calcular áreas e volumes.
Por exemplo, Arquimedes desenvolveu o método da exaustão, que consistia em usar figuras geométricas cada vez mais próximas de um círculo para estimar sua área com altíssima precisão. Essa ideia foi precursora do conceito de limite que conhecemos hoje.
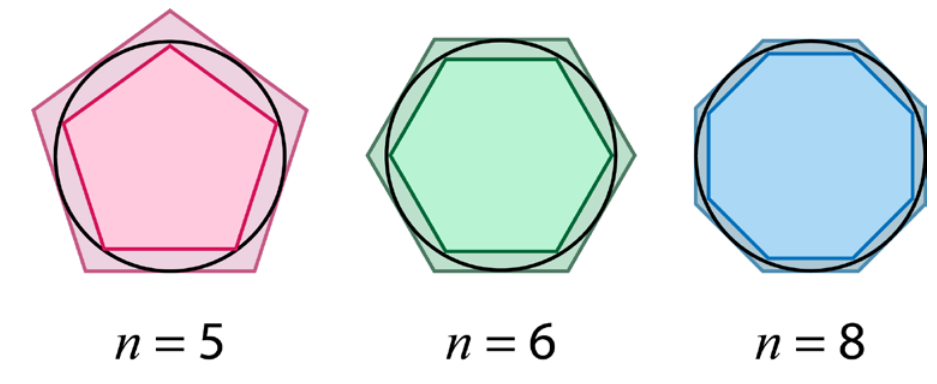
A figura mostra como o uso de polígonos regulares com número crescente de lados permite aproximar a área do círculo.
O Cálculo como ferramenta científica
O cálculo é, antes de tudo, a linguagem matemática das transformações. Em outras palavras, ele lida com tudo aquilo que muda: velocidade, crescimento, diminuição, fluxo, variações…
Por isso, podemos definir o cálculo como:
“a forma científica de lidar com as transformações que ocorrem no mundo físico.”
A importância do limite
No coração do cálculo está o conceito de limite. Quando se fala em derivadas ou integrais, estamos sempre nos referindo a limites de alguma forma.
Veja um exemplo clássico:
A área do círculo e o número π
Considere uma circunferência de raio RRR. Podemos aproximar a área do círculo utilizando a área de um polígono regular de nnn lados inscrito na circunferência. Quanto maior for nnn, mais precisa será a aproximação.
Quando nnn tende ao infinito, a área do polígono tende à área do círculo. Assim, a área AAA pode ser expressa como:
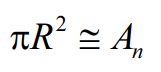
Com isso, o número π pode ser definido como:
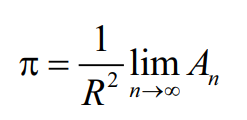
O número e: outro limite essencial
Outro número fundamental na matemática é o número eee, que também é definido por um limite. Ele aparece em fenômenos como crescimento populacional, juros compostos e decaimento radioativo.
Uma definição comum é:
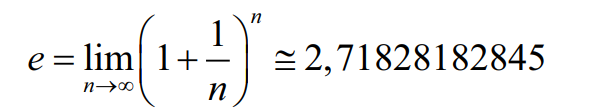
Ou, de forma mais geral:
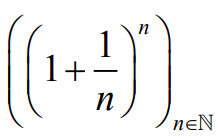
Esse número irracional é aproximadamente igual a 2,71828 e tem infinitas casas decimais não periódicas.
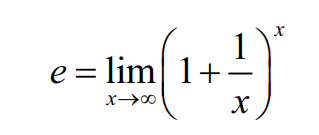
Por que estudar cálculo?
Estudar cálculo é muito mais do que manipular símbolos ou resolver fórmulas. É desenvolver a capacidade de:
- Analisar mudanças;
- Resolver problemas com variáveis;
- Modelar situações do mundo real com precisão matemática;
- Compreender fenômenos naturais e sociais.
Conclusão
O estudo do cálculo começa pelo entendimento do limite, uma ferramenta conceitual que nos permite tratar situações com variações contínuas ou infinitamente pequenas. É a partir dele que toda a estrutura do cálculo diferencial e integral é construída.
Neste artigo, vimos como o cálculo surgiu, sua divisão em dois grandes ramos e a centralidade dos conceitos de limite, π e eee na construção do pensamento matemático moderno.






















