O Discriminante Delta (Δ)
Entenda a importância do discriminante Δ na resolução de equações do segundo grau e na análise da função quadrática.
O que é o Discriminante Delta?
O discriminante, representado pela letra grega Δ (delta), é um valor calculado a partir dos coeficientes de uma equação do segundo grau. Ele desempenha um papel fundamental para determinar o número de raízes reais e distintas de uma função quadrática.
Δ = b² – 4ac
Interpretação do Discriminante
Dependendo do valor de Δ, temos diferentes cenários para a equação quadrática:
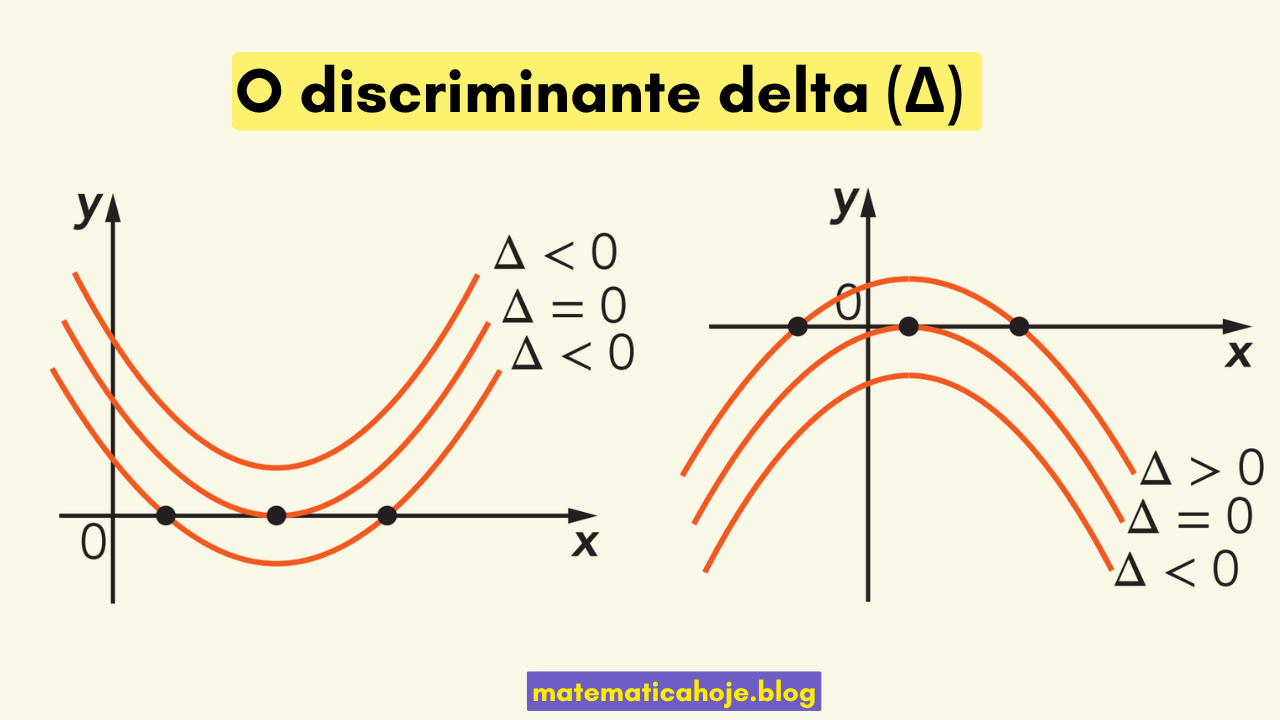
- Δ > 0: a equação possui duas raízes reais e distintas. O gráfico da parábola corta o eixo x em dois pontos diferentes.
- Δ = 0: a equação possui apenas uma raiz real (raiz dupla). A parábola toca o eixo x em um único ponto (no vértice).
- Δ < 0: a equação não possui raízes reais. O gráfico da parábola não corta o eixo x.
Relação com a Função Quadrática
O discriminante está diretamente ligado ao gráfico da função quadrática e sua análise. Ele ajuda a compreender a variação de sinal, a posição da parábola em relação ao eixo x e a existência de soluções reais. Em conjunto com a concavidade (determinada pelo coeficiente a), conseguimos interpretar toda a estrutura do gráfico.
Tenha todas as fórmulas de matemática organizadas em um só lugar.
Baixe agora o eBook Fórmulas Matemática
Exemplos Resolvidos
Exemplo 1: Analise a equação x² – 5x + 6 = 0 determinando o valor de Δ e o número de raízes.
Coeficientes: a = 1, b = -5, c = 6
Δ = (-5)² – 4·1·6 = 25 – 24 = 1
Como Δ > 0, a equação possui duas raízes reais e distintas.
Exemplo 2: Determine Δ para a equação 2x² + 4x + 2 = 0 e interprete o resultado.
Coeficientes: a = 2, b = 4, c = 2
Δ = (4)² – 4·2·2 = 16 – 16 = 0
Como Δ = 0, a equação possui uma raiz real (raiz dupla).
Exemplo 3: Verifique Δ na equação x² + x + 5 = 0.
Coeficientes: a = 1, b = 1, c = 5
Δ = 1² – 4·1·5 = 1 – 20 = -19
Como Δ < 0, a equação não possui raízes reais.
Conclusão
O discriminante Δ é um dos conceitos mais importantes da função quadrática, pois define se a equação terá duas, uma ou nenhuma solução real. Ele está intimamente ligado ao formato e à posição da parábola em relação ao eixo x, sendo essencial em problemas de imagem da função quadrática, vértice e estudo do sinal.













