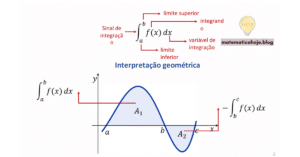
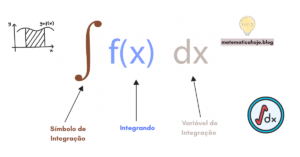
O Triângulo de Pascal, também conhecido como Triângulo de Tartaglia, é uma tabela organizada de forma simples e eficiente para representar os coeficientes binomiais. Ele tem aplicações fundamentais em várias áreas da matemática, como álgebra, combinatória e probabilidade. Vamos explorar o conceito, como ele é construído e suas principais propriedades.
Blaise Pascal (1623-1662) foi um matemático, físico, filósofo e inventor francês, conhecido por suas contribuições pioneiras em diversas áreas do conhecimento. Na matemática, destacou-se pela criação do Triângulo de Pascal, uma ferramenta fundamental na análise combinatória e no cálculo de probabilidades. Na física, realizou estudos sobre pressão e fluidos, estabelecendo as bases da hidrostática, com a famosa Lei de Pascal. Além disso, desenvolveu uma das primeiras calculadoras mecânicas, a Pascalina, e deixou um legado filosófico com sua obra “Pensamentos”, que aborda temas sobre a existência humana e a fé. Sua genialidade interdisciplinar o coloca entre as grandes mentes da história.
O Que é o Triângulo de Pascal?
O Triângulo de Pascal é uma disposição triangular onde cada linha representa os coeficientes binomiais associados ao desenvolvimento de (x + a)n. A tabela é estruturada da seguinte forma:
- A primeira linha (n = 0) contém apenas o número 1.
- A segunda linha (n = 1) contém os coeficientes 1 e 1, correspondentes a (x + a)1 = x + a
- A terceira linha (n = 2) contém 1, 2 e 1, representando (x + a)2 = x2 + 2ax + a2
- E assim por diante, com cada linha contendo n + 1 elementos.
O Triângulo de Pascal é visualmente representado assim:
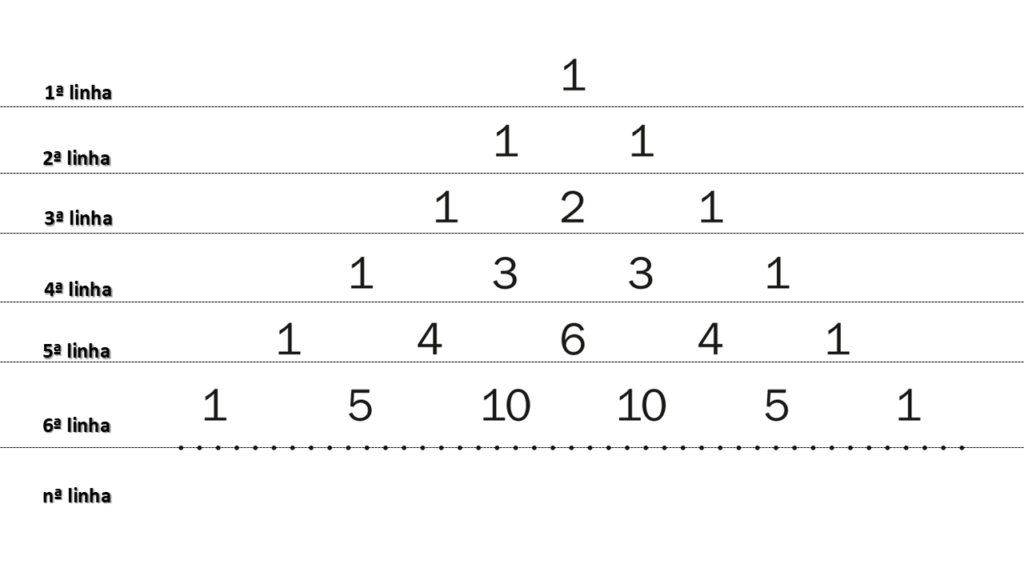
Como Construir o Triângulo de Pascal
A construção do triângulo segue três regras básicas:
O primeiro e o último número de cada linha é sempre 1.
Isso ocorre porque os coeficientes binomiais
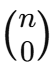
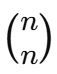
são sempre iguais a 1, independentemente do valor de n.
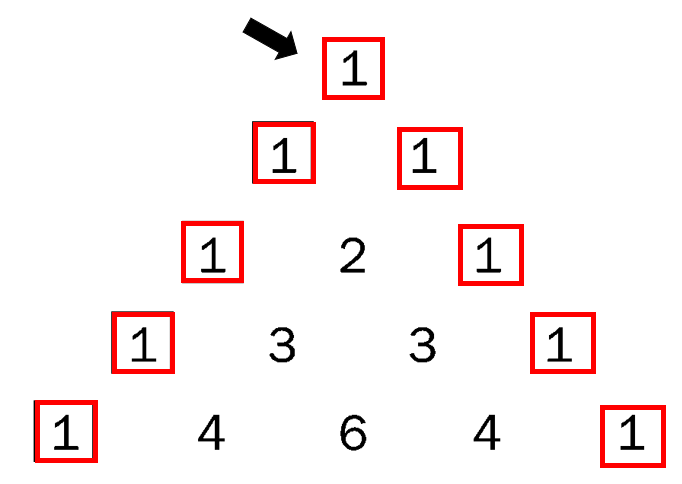
Cada número interno é a soma dos dois números diretamente acima dele na linha anterior.
- Essa propriedade é conhecida como a relação de Stifel:
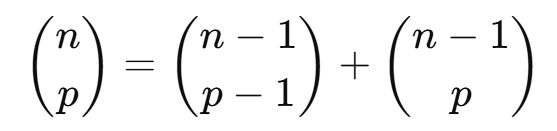
A partir da 3ª Iinha, cada elemento (com exceção do primeira e do último) é a
soma dos dois elementos da linha anterior, imediatamente acima dele.
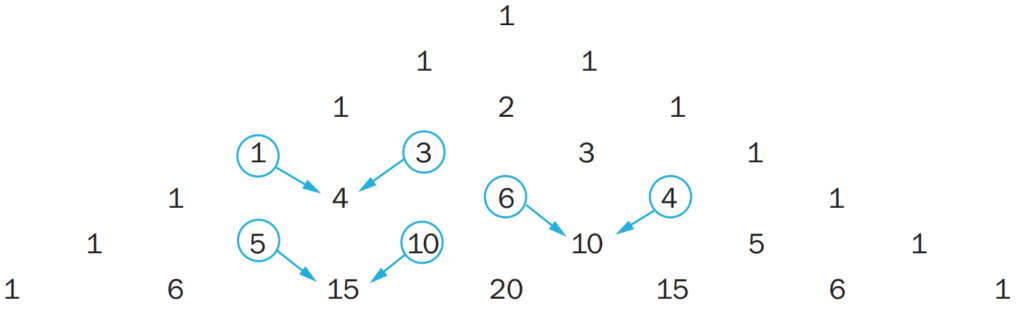
Exemplo
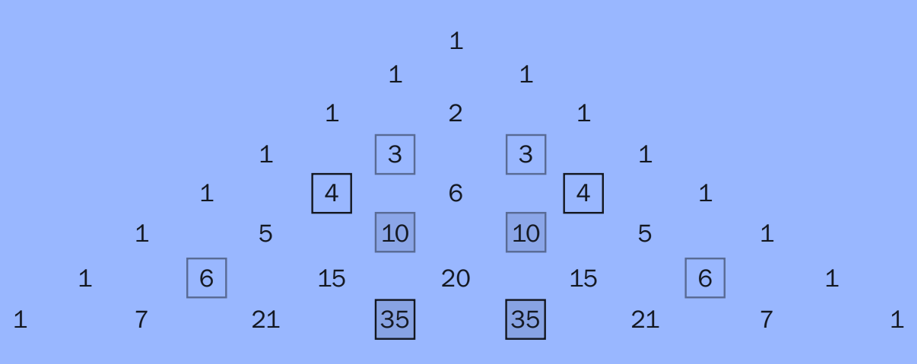
Coeficientes equidistantes dos extremos de uma linha são iguais.
- Isso reflete a simetria do triângulo:
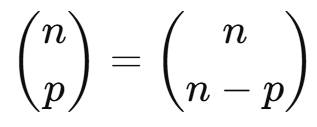
Notemos que:
A 1ª linha do triângulo contém os coeficientes do desenvolvimento de (x + a)0
.
A 2ª linha do triângulo contém os coeficientes do desenvolvimento de (x + a)1
.
A 3ª linha do triângulo contém os coeficientes do desenvolvimento de (x + a)2
.
E assim por diante.
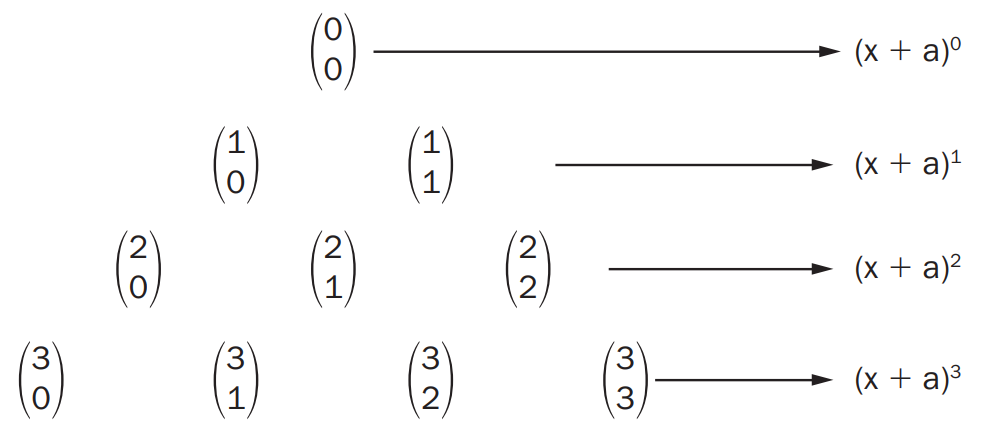
Aplicações do Triângulo de Pascal
1. Expansão de Binômios
Os números no triângulo correspondem aos coeficientes dos termos no desenvolvimento de (x + a)n. Por exemplo:
- Para (x + a)3, a terceira linha (1, 3, 3, 1) dá:
(x + a)3 = x3 + 3x2a + 3xa2 + a3
2. Análise Combinatória
Os números presentes no Triângulo de Pascal representam os coeficientes binomiais, que indicam o número de maneiras de escolher k elementos de um conjunto com n elementos na Análise Combinatória, conhecido como combinações. Essa conexão é evidente na fórmula combinatória:
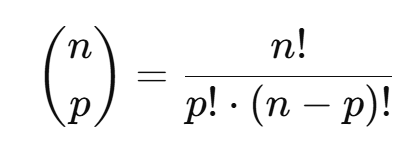
Por exemplo, na 5ª linha do triângulo (1, 5, 10, 10, 5, 1), os valores correspondem ao número de combinações possíveis ao escolher 0, 1, 2, 3, 4 ou 5 elementos de um conjunto com 5 elementos.
3. Probabilidade
Na probabilidade, o Triângulo de Pascal é amplamente utilizado em problemas que envolvem distribuições binomiais, como calcular a probabilidade de obter um número específico de sucessos em n ensaios de Bernoulli. Por exemplo:
- Ao lançar uma moeda 5 vezes, a probabilidade de obter exatamente 3 caras é:
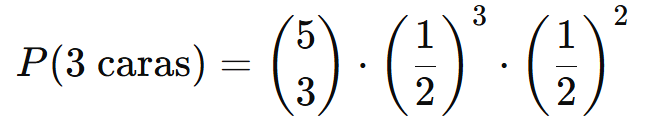
Aqui, o coeficiente binomial (53) = 10, obtido no Triângulo de Pascal, representa o número de combinações possíveis para 3 caras em 5 lançamentos.
Propriedades Importantes do Triângulo de Pascal
Primeiro e Último Elementos Igual a 1
O primeiro e o último número de cada linha são sempre iguais a 1
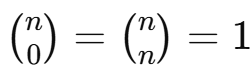
Relação de Stifel
Cada número interno é a soma dos dois números imediatamente acima dele:
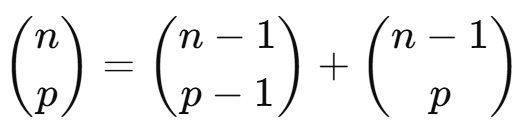
Simetria
Os números em uma linha são simétricos em relação ao meio:

A Soma de Cada Linha
A soma dos números de uma linha n é 2n. Por exemplo:
Linha 2 (1, 2, 1): 1+2+1 = 4 = 22
Linha 3 (1, 3, 3, 1): 1+3+3+1=8=23
Triângulo de Pascal e Binômio de Newton
O Triângulo de Pascal e o Binômio de Newton estão intimamente relacionados, pois os coeficientes binomiais presentes no triângulo correspondem exatamente aos coeficientes dos termos no desenvolvimento de (x + a)n. Cada linha do triângulo representa os coeficientes do binômio para um valor específico de n. Por exemplo, a 4ª linha do triângulo (1, 4, 6, 4, 1) fornece os coeficientes para (x + a)4 = x4 + 4x3a + 6x2a2 + 4xa3 + a4. Essa relação facilita a expansão de binômios sem necessidade de cálculos complexos, tornando o Triângulo de Pascal uma ferramenta prática para aplicar a fórmula do Binômio de Newton.
Exemplo Prático
Expansão de (x + 2)4:
Usando a 5ª linha do triângulo (1, 4, 6, 4, 1), temos:
(x + 2)4 = 1⋅x4 + 4⋅x3⋅2 + 6⋅x2⋅22 + 4⋅x⋅23 + 1⋅24
(x + 2)4 = x4 + 8x3 + 24x2 + 32x + 16
O Triângulo de Pascal possui uma relação direta e fundamental com a probabilidade e a análise combinatória, formando a base para diversas aplicações matemáticas.
O Triângulo de Pascal serve como um ponto de convergência entre a análise combinatória e a probabilidade. Ele fornece os coeficientes binomiais necessários para expandir potências no Binômio de Newton, calcular combinações em problemas de contagem e determinar probabilidades em experimentos probabilísticos. Essa versatilidade faz do Triângulo de Pascal uma ferramenta indispensável na matemática, simplificando cálculos e permitindo uma compreensão visual das relações matemáticas.
Conclusão
O Triângulo de Pascal é uma ferramenta matemática simples, mas extremamente útil, que conecta álgebra, combinatória e probabilidade. Ele permite calcular coeficientes binomiais de forma eficiente e compreender melhor os padrões matemáticos em diferentes contextos. Aprender a usá-lo não só facilita cálculos complexos, mas também aprimora o entendimento das inter-relações fundamentais na matemática.