Enunciado: Na figura observamos três caminhos A, B e C, destacados em vermelho. Eles ligam o topo de uma pirâmide regular de base quadrada a um vértice em sua base, passando por arestas e trechos paralelos à base.
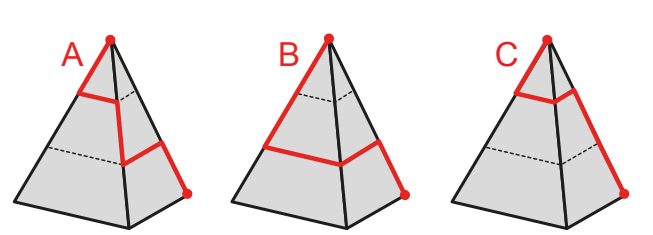
Se a distância percorrida no caminho A é \(a\), no caminho B é \(b\) e no caminho C é \(c\), qual das seguintes afirmações é verdadeira?
- (A) \(a = b = c\)
- (B) \(c < b < a\)
- (C) \(a < b < c\)
- (D) \(a < c < b\)
- (E) \(c < a < b\)
Ver Solução
Entendendo o enunciado: A questão envolve comparar os comprimentos de diferentes trajetos entre o topo de uma pirâmide e pontos em sua base, considerando que alguns segmentos são arestas da pirâmide e outros são paralelos à base.
Resolução:
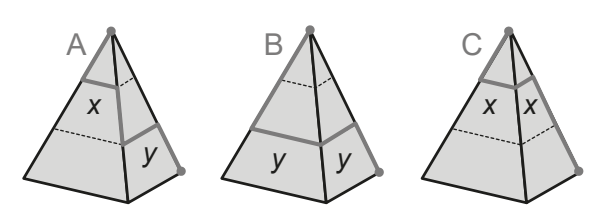
Nos três caminhos, os segmentos ao longo das arestas laterais da pirâmide têm, no total, o mesmo comprimento: o da aresta lateral da pirâmide. Representando por \(x\) o comprimento dos segmentos paralelos à base mais próximos aos vértices e por \(y\) o comprimento dos mais distantes, temos:
- \(a = x + y + \text{aresta lateral da pirâmide}\)
- \(b = 2y + \text{aresta lateral da pirâmide}\)
- \(c = 2x + \text{aresta lateral da pirâmide}\)
Como \(x < y\), temos \(2x < x + y < 2y\), portanto:
\(c < a < b\)
Gabarito: Letra E
🧠 Mapas Mentais de Matemática





















