OBMEP 2024 – Nível 3 – Questão 13
Enunciado:
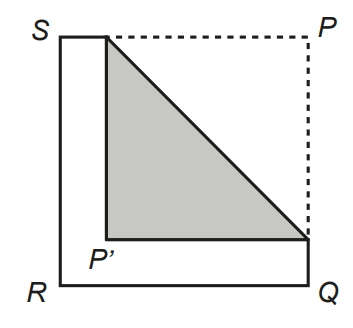
Uma folha quadrada de papel, branca de um lado e cinza do outro, tem área igual a 75 cm². A folha é dobrada de modo que o vértice P seja levado a um ponto P’ da diagonal PR, conforme a figura. Depois da dobra, as partes branca e cinza visíveis ficaram com a mesma área. Qual é a distância, em centímetros, do ponto P’ até o ponto P?
(A) 7,0
(B) 6,0
(C) 7,5
(D) 5,0
(E) 10,0
Ver Solução
Entendendo o enunciado: A folha foi dobrada, e a área visível branca ficou igual à área visível cinza. Como a área total é 75 cm², cada parte visível representa \( \frac{75}{3} = 25 \, \text{cm}^2 \).
Vamos resolver:
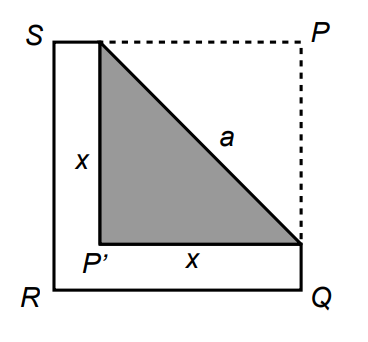
O triângulo cinza formado tem catetos de comprimento x e área igual a:
\[ \frac{x^2}{2} = 25 \Rightarrow x^2 = 50 \Rightarrow x = \sqrt{50} \]
Aplicando o Teorema de Pitágoras para calcular a hipotenusa a (que representa a distância de \(P\) até \(P’\)):
\[ a = \sqrt{x^2 + x^2} = \sqrt{50 + 50} = \sqrt{100} = \boxed{10} \]
Resposta correta: (E) 10,0