OBMEP 2024 – Nível 3 – Questão 5
Enunciado:
O desenho a seguir representa um mapa que tem 7 cidades, representadas por pontos, e 5 estradas, representadas por curvas. Qual é o menor número de estradas que devem ser incluídas no desenho para que de cada cidade parta o mesmo número de estradas?
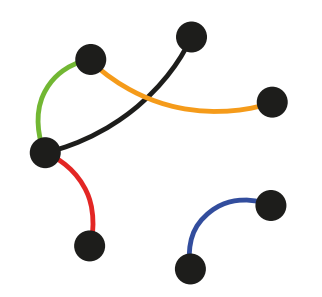
Alternativas:
- (A) 9
- (B) 5
- (C) 4
- (D) 10
- (E) 11
Ver Solução
1. Análise inicial:
Temos 7 cidades (vértices) e 5 estradas (arestas).
O objetivo é que todas as cidades tenham o mesmo número de estradas partindo delas (mesmo grau).
2. Tentativa com grau 3:
Se cada cidade tivesse grau 3, teríamos:
\[
7 \times 3 = 21 \text{ conexões distintas}
\]
Como cada estrada conecta 2 cidades, o número total de estradas seria:
\[
\frac{21}{2} = 10{,}5
\]
O que não é possível, pois o número de estradas precisa ser inteiro.
3. Tentativa com grau 4:
Agora, suponha 4 estradas por cidade:
\[
7 \times 4 = 28 \text{ conexões} \Rightarrow \frac{28}{2} = 14 \text{ estradas}
\]
Isso é viável.
4. Total a adicionar:
Já temos 5 estradas. Precisamos de:
\[
14 – 5 = \boxed{9} \text{ estradas}
\]
Resposta correta: (A) 9
🧠 Mapas Mentais de Matemática





















