OBMEP 2024 – Nível 3 – Questão 6
Enunciado:
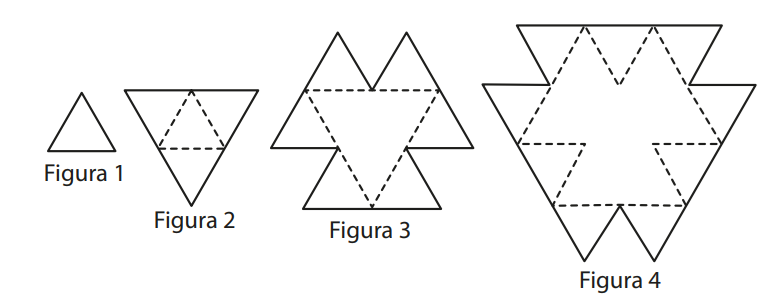
Na sequência de figuras formadas por triângulos equiláteros idênticos, mostrada abaixo, cada figura é formada pela figura anterior acrescida da menor quantidade possível de triângulos que escondem o perímetro da figura anterior. Quantos triângulos devem ser adicionados à Figura 9 para se obter a Figura 10?
Alternativas:
- (A) 24
- (B) 21
- (C) 30
- (D) 27
- (E) 18
Ver Solução
1. Observando o padrão:
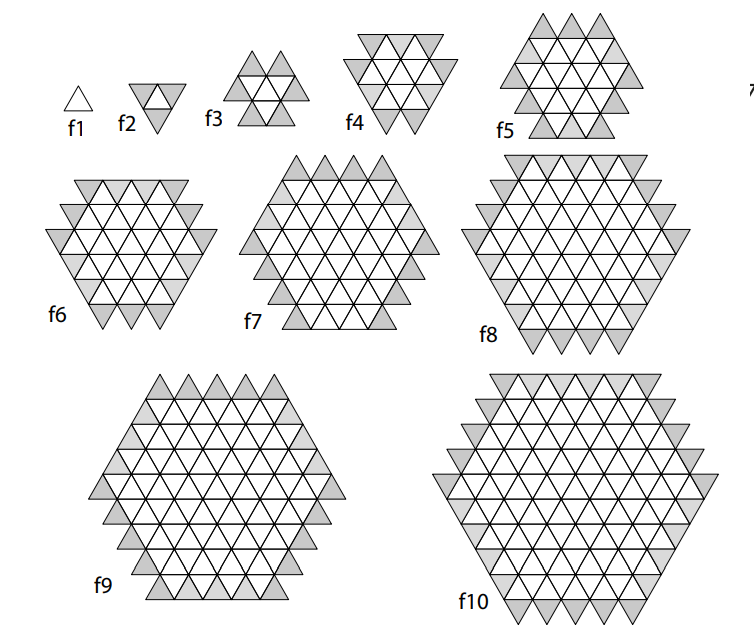
Entre uma figura e a próxima, a quantidade de triângulos adicionados segue a progressão aritmética de razão 3:
\[ 3,\ 6,\ 9,\ 12,\ 15,\ 18,\ 21,\ 24,\ 27,\ \dots \]
Esses valores correspondem ao número de triângulos adicionados para formar da figura 2 até a 10:
- Figura 2: +3
- Figura 3: +6
- Figura 4: +9
- …
- Figura 10: +27
2. Justificativa matemática:
O número de triângulos adicionados à figura \(n\) para formar a figura \(n+1\) segue a fórmula:
\[ T(n+1) = T(n) + 3n \]Para ir da Figura 9 para a 10:
\[ T(10) = T(9) + 3 \times 9 = T(9) + 27 \]Portanto, devem ser adicionados: 27 triângulos
Resposta correta: (D) 27
🧠 Mapas Mentais de Matemática





















