Nesta seção, exploramos como os limites surgem ao tentarmos encontrar a tangente de uma curva ou a velocidade de um objeto em um instante específico.
O Problema da Tangente
A palavra “tangente” vem do latim tangens, que significa “tocando”. Assim, uma reta tangente é uma linha que toca uma curva em apenas um ponto, sem cruzá-la nesse ponto. Em termos simples, uma reta tangente à curva tem a mesma direção que a curva no ponto de contato.
Para ilustrar, considere a ideia geométrica clássica de Euclides: a tangente é uma reta que intercepta um círculo em apenas um ponto. Para curvas mais complexas, usamos limites para definir precisamente essa tangente.
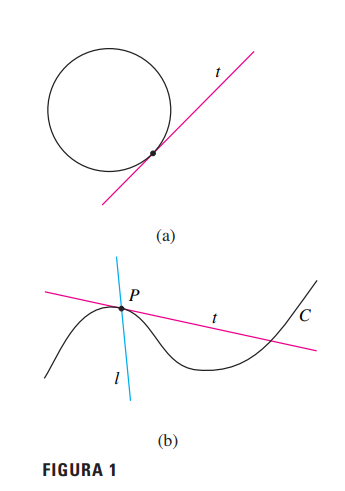
A Figura 1(a) mostra a tangente a um círculo. A Figura 1(b) mostra uma curva mais geral, onde linhas secantes se aproximam da tangente conforme o ponto se aproxima do ponto de tangência.
Cálculo 1 – Teoria e Exercícios
Exemplo 1: Encontrando a tangente à parábola
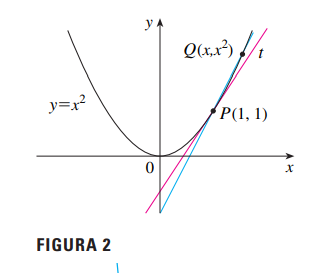
Queremos encontrar a equação da reta tangente à parábola \( y = x^2 \) no ponto \( P(1,1) \).
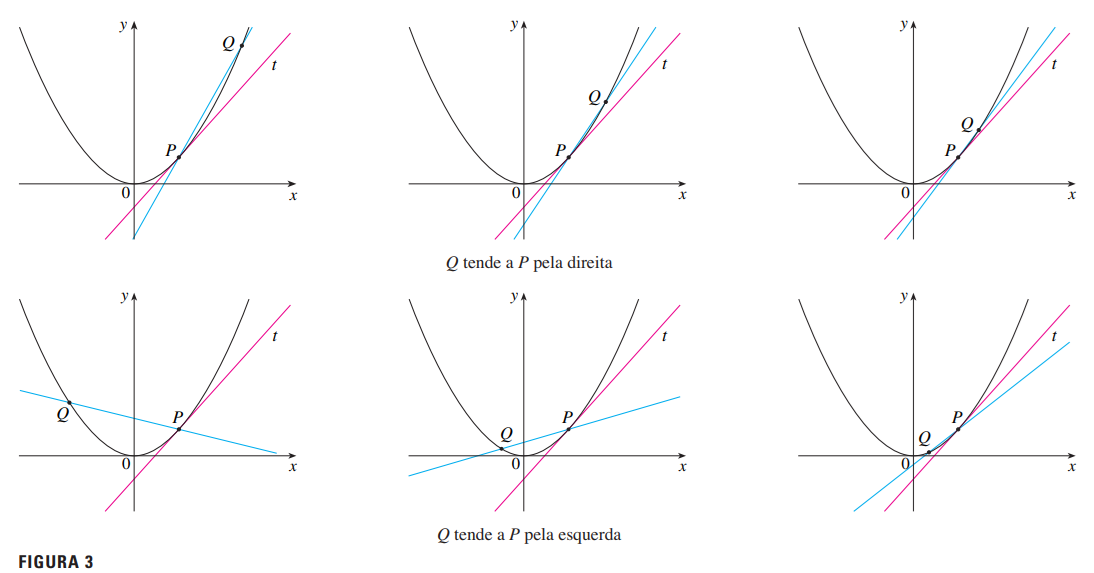
Consideramos outro ponto \( Q(x, x^2) \) sobre a parábola e calculamos a inclinação da reta secante:
\[ m_{PQ} = \frac{x^2 – 1}{x – 1} \]
Por exemplo, para \( x = 1{,}5 \):
\[ m_{PQ} = \frac{2{,}25 – 1}{1{,}5 – 1} = \frac{1{,}25}{0{,}5} = 2{,}5 \]
Repetindo esse cálculo com valores cada vez mais próximos de 1, observamos que \( m_{PQ} \) tende a 2. Assim:
\[ \lim_{x \to 1} \frac{x^2 – 1}{x – 1} = 2 \]
A equação da reta tangente, com coeficiente angular 2 e passando por \( P(1,1) \), é:
\[ y – 1 = 2(x – 1) \quad \text{ou} \quad y = 2x – 1 \]
Estimando Tangentes com Dados Experimentais
Funções nem sempre são dadas por fórmulas; muitas são descritas por dados experimentais.
Exemplo 2: Carga de um capacitor
Considere a carga \( Q \) em um capacitor ao longo do tempo \( t \), conforme a tabela e o gráfico abaixo.
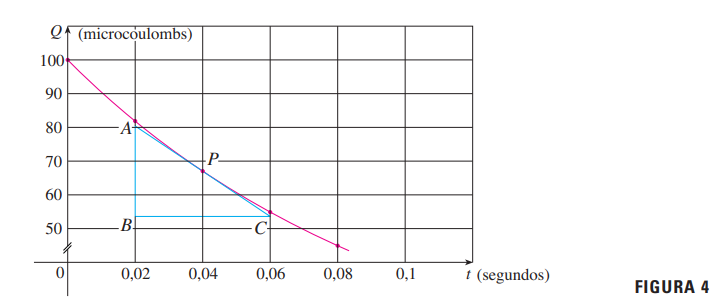
Para estimar a inclinação da reta tangente no ponto \( P(0{,}04, 67{,}03) \), usamos a reta secante com o ponto \( R(0{,}00, 100{,}00) \):
\[ m_{PR} = \frac{67{,}03 – 100{,}00}{0{,}04 – 0{,}00} = -824{,}25 \]
Repetindo com outros pontos, obtemos inclinações como -742, -675 etc. A média fornece uma boa estimativa da inclinação da tangente: cerca de -670 microcoulombs por segundo.
Cálculo 1 – Teoria e Exercícios
O Problema da Velocidade
A velocidade média é a taxa de variação da posição com o tempo. Para descobrir a velocidade em um instante específico, usamos limites.
Exemplo 3: Bola caindo da Torre CN
A posição \( s(t) \) da bola é dada por:
\[ s(t) = 4{,}9t^2 \]
Queremos a velocidade no instante \( t = 5 \). Usamos:
\[ \text{velocidade média} = \frac{s(t) – s(5)}{t – 5} = \frac{4{,}9t^2 – 122{,}5}{t – 5} \]
Para valores de \( t \) próximos de 5 (como 5,1; 5,01; 5,001), a velocidade média se aproxima de 49 m/s. Assim:
\[ \lim_{t \to 5} \frac{s(t) – s(5)}{t – 5} = 49 \text{ m/s} \]
Conexão entre Tangente e Velocidade
O problema da velocidade é um caso especial do problema da tangente. Quando consideramos a posição como uma função do tempo, a velocidade instantânea é a inclinação da reta tangente ao gráfico da posição.
A equação da reta secante entre \( P(a, s(a)) \) e \( Q(a + h, s(a + h)) \) é:
\[ m_{PQ} = \frac{s(a + h) – s(a)}{h} \]
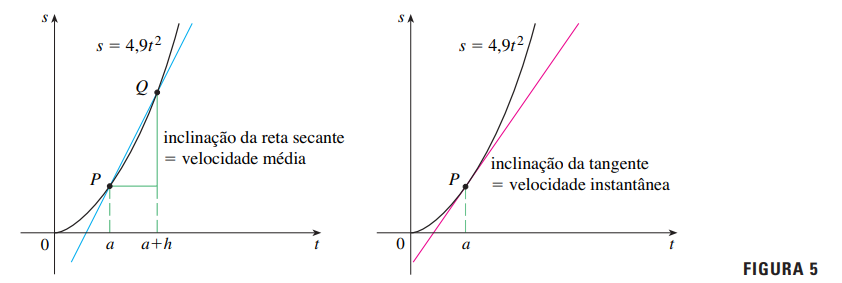
Esse é o mesmo tipo de cálculo que usamos para a tangente. Assim, os dois problemas estão intimamente conectados.
Conclusão
O estudo da tangente e da velocidade leva naturalmente ao conceito de limite. Esses exemplos mostram como limites são essenciais para entender taxas de variação instantâneas e a geometria das curvas. No cálculo diferencial, esse conceito será aprofundado com a definição formal de derivada.
Cálculo 1 – Teoria e Exercícios
Exercícios Resolvidos: Problemas de Tangente e Velocidade
Questão 1
Um tanque com capacidade para 1.000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume \( V \) de água remanescente no tanque (em litros) após \( t \) minutos:
| t (min) | 5 | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|---|
| V (L) | 694 | 444 | 250 | 111 | 28 | 0 |
- Se \( P = (15, 250) \), calcule as inclinações das retas secantes \( PQ \), onde \( Q \) corresponde aos valores de \( t = 5, 10, 20, 25, 30 \).
- Estime a inclinação da reta tangente em \( P \) pela média de duas retas secantes próximas.
- Use o gráfico para estimar a taxa de escoamento após 15 minutos.
Ver Solução
\( m_{PQ}(5) = \frac{250 – 694}{15 – 5} = -44{,}4 \)
\( m_{PQ}(10) = \frac{250 – 444}{5} = -38{,}8 \)
\( m_{PQ}(20) = \frac{111 – 250}{5} = -27{,}8 \)
\( m_{PQ}(25) = \frac{28 – 250}{10} = -22{,}2 \)
\( m_{PQ}(30) = \frac{0 – 250}{15} = -16{,}67 \)
(b) Média entre -27,8 e -22,2:
\( \frac{-27{,}8 + (-22{,}2)}{2} = -25 \)
(c) A estimativa gráfica é coerente com o valor de -25 L/min.
Questão 2
Um monitor é usado para medir os batimentos cardíacos de um paciente após uma cirurgia.
| t (min) | 36 | 38 | 40 | 42 | 44 |
|---|---|---|---|---|---|
| Batimentos | 2530 | 2661 | 2806 | 2948 | 3080 |
Use os dados da tabela para estimar a taxa de variação dos batimentos após 42 minutos:
- \( t = 36 \) e \( t = 42 \)
- \( t = 38 \) e \( t = 42 \)
- \( t = 40 \) e \( t = 42 \)
- \( t = 42 \) e \( t = 44 \)
Ver Solução
(b) \( m = \frac{2948 – 2661}{4} = 71{,}75 \)
(c) \( m = \frac{2948 – 2806}{2} = 71 \)
(d) \( m = \frac{3080 – 2948}{2} = 66 \)
Conclusão: A taxa de variação dos batimentos está entre 66 e 72 bpm/min.
Questão 3
O ponto \( P(2, -1) \) está sobre a curva \( y = \frac{1}{1 – x} \).
- Calcule a inclinação da secante \( PQ \) com \( Q = (x, f(x)) \) para os seguintes valores de \( x \): 1,5; 1,9; 1,99; 1,999; 2,5; 2,1; 2,01; 2,001.
- Estime a inclinação da reta tangente em \( P \).
- Encontre a equação da reta tangente em \( P \).
Ver Solução
\( m(1{,}5) \approx -3{,}555556 \)
\( m(1{,}9) \approx -4{,}736842 \)
\( m(1{,}99) \approx -4{,}974874 \)
\( m(1{,}999) \approx -4{,}9975 \)
\( m(2{,}5) \approx -2{,}222222 \)
\( m(2{,}1) \approx -3{,}174603 \)
\( m(2{,}01) \approx -4{,}975124 \)
\( m(2{,}001) \approx -4{,}9975 \)
(b) A inclinação da tangente é aproximadamente \( -5 \).
(c) Equação da reta tangente:
\( y + 1 = -5(x – 2) \Rightarrow y = -5x + 9 \)













