Pirâmide — Volume, Apótema, Área Lateral e Área Total (com Exercícios Resolvidos)
Domine as fórmulas de pirâmides regulares: relação entre apótema da base e apótema lateral, cálculo do volume, da superfície lateral e da área total, com exemplos passo a passo.
O que é uma Pirâmide?
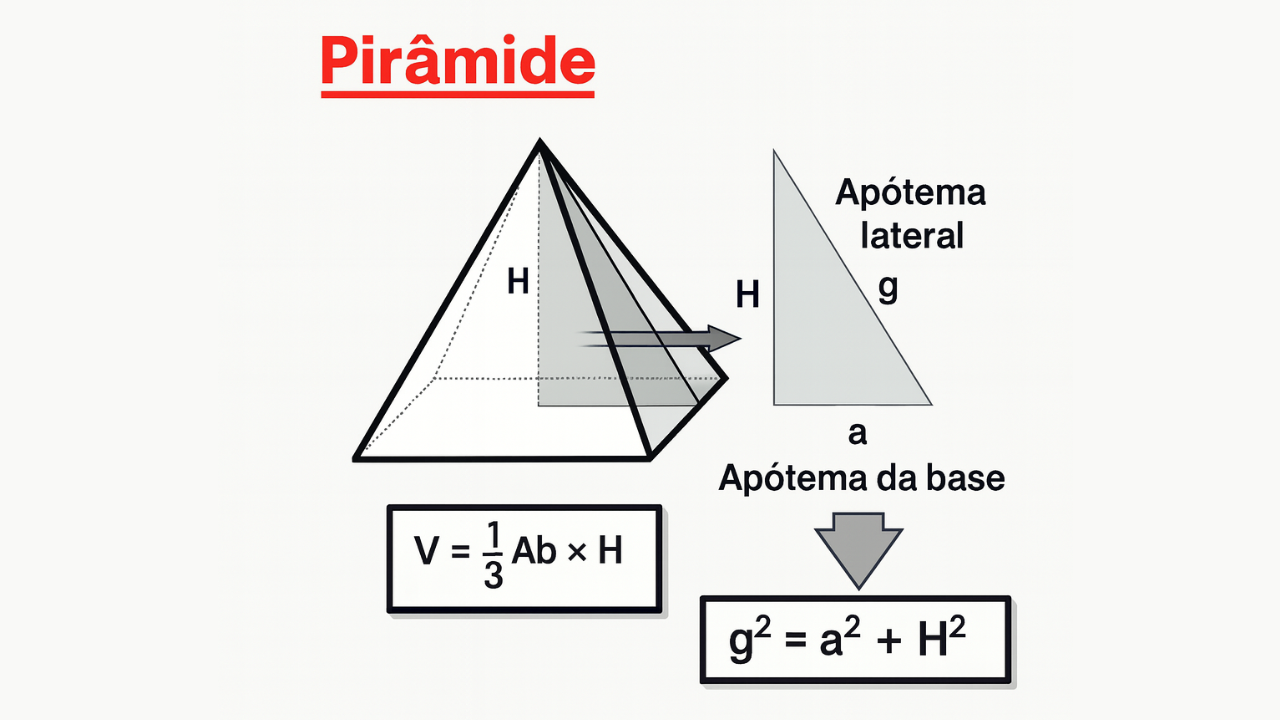
Pirâmide é um sólido geométrico formado por uma base poligonal e faces laterais triangulares que se encontram em um vértice comum. Nas provas, é comum trabalhar com a pirâmide regular, cuja base é um polígono regular e o segmento que liga o vértice ao centro da base é perpendicular ao plano da base.
- H: altura da pirâmide (do vértice ao centro da base).
- a: apótema da base (raio do círculo inscrito na base regular).
- g: apótema lateral (altura de cada face triangular).
Na pirâmide regular, vale a relação do triângulo retângulo formado por \(H\), \(a\) e \(g\): \(g^2 = a^2 + H^2\).
Fórmulas Essenciais
Volume
\( V = \dfrac{1}{3}\,A_b \cdot H \)
Áreas
Área lateral: \( A_L = \dfrac{P_b \cdot g}{2} \)
Área total: \( A_T = A_b + A_L \)
Aqui, \(P_b\) é o perímetro da base e \(g\) é o apótema lateral.
Relação métrica (pirâmide regular)
\( g^2 = a^2 + H^2 \)
Reforce com os Mapas Mentais e pratique mais no Banco de Questões.
Exemplos Resolvidos
Exemplo 1 — Volume
Enunciado. Uma pirâmide quadrangular regular tem base quadrada de lado \(l=6\) cm e altura \(H=10\) cm. Calcule o volume.
Ver solução
\( A_b = l^2 \)
\( A_b = 6^2 \)
\( A_b = 36\ \text{cm}^2 \)
\( V = \dfrac{1}{3} \cdot A_b \cdot H \)
\( V = \dfrac{1}{3} \cdot 36 \cdot 10 \)
\( V = \dfrac{360}{3} \)
\( V = \mathbf{120\ \text{cm}^3} \)
Exemplo 2 — Área Lateral e Total
Enunciado. Numa pirâmide regular de base hexagonal, o lado da base é \(s=5\) cm, o apótema lateral é \(g=9\) cm. Encontre \(A_L\) e \(A_T\). (Use \(A_b = \dfrac{P_b \cdot a}{2}\); para hexágono regular, \(a = \dfrac{\sqrt{3}}{2}s\)).
Ver solução
\( P_b = 6s \)
\( P_b = 6 \cdot 5 \)
\( P_b = 30\ \text{cm} \)
\( A_L = \dfrac{P_b \cdot g}{2} \)
\( A_L = \dfrac{30 \cdot 9}{2} \)
\( A_L = \dfrac{270}{2} \)
\( A_L = \mathbf{135\ \text{cm}^2} \)
\( a = \dfrac{\sqrt{3}}{2}s \)
\( a = \dfrac{\sqrt{3}}{2}\cdot 5 \)
\( a = \dfrac{5\sqrt{3}}{2} \)
\( A_b = \dfrac{P_b \cdot a}{2} \)
\( A_b = \dfrac{30 \cdot \frac{5\sqrt{3}}{2}}{2} \)
\( A_b = \dfrac{150\sqrt{3}}{4} \)
\( A_b = \mathbf{37{,}5\sqrt{3}\ \text{cm}^2} \) (≈ \(64{,}95\ \text{cm}^2\))
\( A_T = A_b + A_L \)
\( A_T \approx 64{,}95 + 135 \)
\( A_T \approx \mathbf{199{,}95\ \text{cm}^2} \) (≈ \(200\ \text{cm}^2\))
Exemplo 3 — Encontrando \(g\) pela relação métrica
Enunciado. Em uma pirâmide quadrangular regular, a altura é \(H=12\) cm e o lado da base é \(l=10\) cm. Calcule o apótema lateral \(g\).
Ver solução
Para base quadrada: \( a = \dfrac{l}{2} \)
\( a = \dfrac{10}{2} \)
\( a = 5\ \text{cm} \)
\( g^2 = a^2 + H^2 \)
\( g^2 = 5^2 + 12^2 \)
\( g^2 = 25 + 144 \)
\( g^2 = 169 \)
\( g = \mathbf{13\ \text{cm}} \)
📘 eBook Grátis — Fórmulas Matemática
Volume, áreas e relações métricas em um único material para revisar antes de provas e concursos.
➡️ Baixar AgoraExercícios Propostos
Resolva e confira o gabarito em cada questão. Para mais listas, acesse o Banco de Questões e a coleção 10 eBooks.
1) Uma pirâmide quadrangular regular tem \(l=8\) cm e \(H=9\) cm. Calcule o volume.
Ver solução
\( A_b=8^2 \)
\( A_b=64 \)
\( V=\frac{1}{3}A_bH \)
\( V=\frac{1}{3}\cdot64\cdot9 \)
\( V=\frac{576}{3} \)
\( V=\mathbf{192\ \text{cm}^3} \)
2) (Múltipla escolha) Em uma pirâmide regular, \(P_b=48\) cm e \(g=7\) cm. A área lateral é:
- 154 cm²
- 168 cm²
- 336 cm²
- 672 cm²
Ver solução
3) Numa pirâmide quadrada, \(l=12\) cm e \(g=13\) cm. Encontre \(H\).
Ver solução
\( g^2=a^2+H^2 \)
\( 13^2=6^2+H^2 \)
\( 169=36+H^2 \)
\( H^2=133 \Rightarrow H=\mathbf{\sqrt{133}\approx11{,}53\ \text{cm}} \)
4) Uma pirâmide triangular regular tem \(s=10\) cm (lado do triângulo equilátero) e \(H=12\) cm. Calcule o volume. (Use \(A_{\triangle}=\frac{\sqrt{3}}{4}s^2\)).
Ver solução
\( A_b=\frac{\sqrt{3}}{4}\cdot100 \)
\( A_b=25\sqrt{3} \)
\( V=\frac{1}{3}A_bH \)
\( V=\frac{1}{3}\cdot25\sqrt{3}\cdot12 \)
\( V=100\sqrt{3} \approx \mathbf{173{,}21\ \text{cm}^3} \)
5) (Múltipla escolha) A área total de uma pirâmide regular é:
- \(2A_b+A_L\)
- \(A_b+\dfrac{P_b g}{2}\)
- \(\dfrac{P_b a}{2}\)
- \(\dfrac{1}{3}A_b H\)
Ver solução
6) Uma pirâmide quadrada tem \(A_T=290\) cm², \(l=10\) cm e \(g=8\) cm. Encontre \(A_b\) e verifique a coerência.
Ver solução
\( A_L=\frac{P_b g}{2}=\frac{40\cdot8}{2}=160 \)
\( A_T=A_b+A_L \Rightarrow 290=A_b+160 \)
\( A_b=130 \) cm²
Para base quadrada: \( l^2=10^2=100 \) cm² (≠ 130) ⇒ dados implicam base não quadrada ou arredondamentos; se a base for quadrada, \(A_T\) coerente seria \(100+160=260\) cm².
7) Uma pirâmide regular tem \(A_L=120\) cm² e \(P_b=24\) cm. Determine \(g\).
Ver solução
\( 120=\frac{24\cdot g}{2} \)
\( 120=12g \)
\( g=\mathbf{10\ \text{cm}} \)
8) Um telhado em forma de pirâmide quadrangular regular cobre uma base de 8 m × 8 m e tem apótema lateral \(g=5{,}5\) m. Qual a área de telhado (apenas a lateral)?
Ver solução
\( A_L=\frac{P_b g}{2}=\frac{32\cdot5{,}5}{2} \)
\( A_L=\frac{176}{2} \)
\( A_L=\mathbf{88\ \text{m}^2} \)
9) Para uma pirâmide regular com \(H=9\) cm e \(a=4\) cm, calcule \(g\) e a diferença \(g-H\).
Ver solução
\( g^2=4^2+9^2 \)
\( g^2=16+81=97 \)
\( g=\sqrt{97}\approx 9{,}85 \) cm
\( g-H\approx 0{,}85 \) cm
10) (Teoria) Assinale a alternativa falsa:
- Em pirâmides regulares, todas as faces laterais são triângulos isósceles congruentes.
- O apótema lateral é a altura de cada face triangular.
- O volume depende apenas do perímetro da base.
- Em pirâmides regulares, \( g^2=a^2+H^2 \).