Planificação do Octaedro
Planificar um sólido significa desenhar todas as faces num mesmo plano, de forma que possamos recortar, dobrar e colar para reconstruir o objeto 3D. O octaedro regular tem 8 faces em forma de triângulos equiláteros, 12 arestas e 6 vértices. A planificação clássica usa uma faixa com quatro triângulos e mais dois triângulos opostos, totalizando 8 faces.
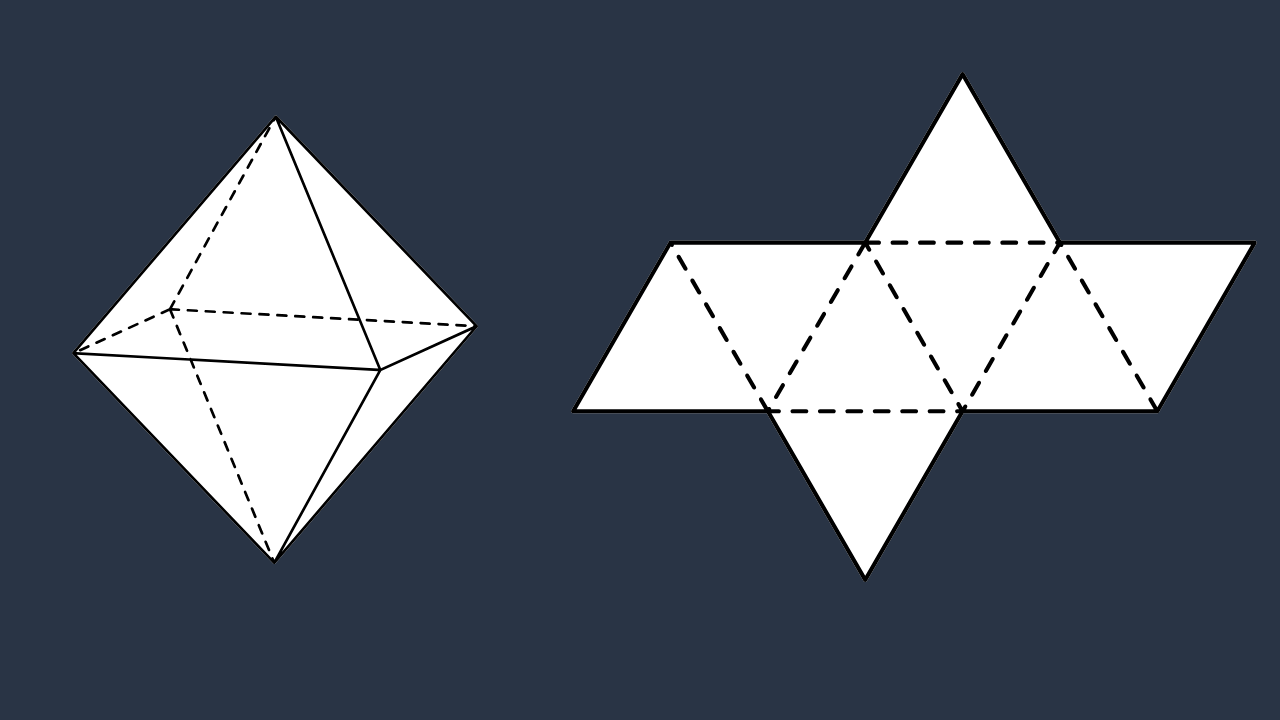
Molde para imprimir
Preparamos um SVG (vetor) com a planificação: cortes em linha contínua e dobras em tracejado, com duas abas de cola.
O arquivo foi gerado com lado do triângulo \(a=50\) mm. Se precisar, ajuste a escala na impressão (por exemplo, 120% tornará \(a=60\) mm). Verifique com régua após imprimir.
Como desenhar a planificação do zero (régua e compasso)
- Escolha o comprimento da aresta \(a\) (o lado do triângulo equilátero).
- Desenhe uma faixa com quatro triângulos equiláteros alternando “ponta para cima/baixo”, todos com lado \(a\).
- Anexe um triângulo acima do segundo e outro abaixo do terceiro triângulo da faixa (ficam em lados opostos).
- Adicione 1–3 abas triangulares ao longo de arestas externas para colagem (altura ~5–8 mm).
- Marque as dobras com tracejado, recorte nas linhas contínuas, dobre e cole.
Altura: \(h_\triangle=\dfrac{\sqrt{3}}{2}a\) • Área: \(A_\triangle=\dfrac{\sqrt{3}}{4}a^2\).
Octaedro: \(A_t=8A_\triangle=2\sqrt{3}\,a^2\) • \(V=\dfrac{\sqrt{2}}{3}a^3\).
Dicas para montagem perfeita
- Papel: 120–180 g/m²; para maquetes grandes use 240 g/m².
- Vinco antes de dobrar: passe levemente um estilete sem cortar nas linhas de dobra (tracejado).
- Cola: branca PVA ou fita dupla-face; segure cada aba por ~20 s.
- Acabamento: comece colando a “banda” de 4 triângulos, depois feche com os dois opostos.
Dimensionamento e papel
Na planificação da figura (faixa de 4 triângulos), a largura total é aproximadamente \(4a\). Em uma folha A4 (largura útil ≈ 19 cm, descontando margens), a maior aresta possível é cerca de \(a\le 4{,}75\) cm. Para caber melhor, reduza margens ou gire o molde.
Cheque de área do molde: área de papel (sem abas) = \(8\cdot\dfrac{\sqrt{3}}{4}a^2=2\sqrt{3}\,a^2\).
Abas: se uma aba tem base \(a\) e altura \(h_{aba}\), então \(A_{aba}=\dfrac{a\,h_{aba}}{2}\).
Quer aprofundar?
- Geometria completa do sólido: Octaedro e Sólidos de Platão.
- Prática com contas: Exercício Octaedro – 15 questões.
Exercícios sobre planificação (com solução)
Nos enunciados, \(a\) é o comprimento da aresta (lado de cada triângulo da planificação).
Q1 — Área do molde
Para \(a=6\) cm, calcule a área total de papel do molde (sem abas).
\(A=2\sqrt{3}\,a^2=2\sqrt{3}\cdot36=72\sqrt{3}\approx 124{,}7\ \text{cm}^2\).
Q2 — Comprimento das dobras
Na planificação “faixa de 4 + 2 opostos”, quantos centímetros de linhas de dobra existem para \(a=8\) cm?
São 5 arestas compartilhadas (3 na faixa + 2 dos opostos). Total \(=5a=40\) cm.
Q3 — Abas de colagem
Serão usadas 6 abas triangulares, cada uma com base \(a=6\) cm e altura \(0{,}5\) cm. Qual a área extra de papel pelas abas?
Área por aba \(=\dfrac{a\,h}{2}=\dfrac{6\cdot0{,}5}{2}=1{,}5\ \text{cm}^2\). Total \(=6\cdot1{,}5=9\ \text{cm}^2\).
Q4 — A maior aresta que cabe no A4
Com largura útil de 19 cm em A4, qual o maior \(a\) que permite encaixar a faixa de 4 triângulos sem girar o molde?
A largura é \(4a\le 19\Rightarrow a\le 4{,}75\ \text{cm}\).
Q5 — Altura de cada triângulo da planificação
Para \(a=7\) cm, determine a altura de cada triângulo equilátero do molde.
\(h_\triangle=\dfrac{\sqrt{3}}{2}a=\dfrac{\sqrt{3}}{2}\cdot7\approx 6{,}062\ \text{cm}\).
Q6 — Escala de impressão
Você tem um molde com \(a=50\) mm (arquivo SVG). Para obter \(a=60\) mm, qual percentual de escala deve aplicar na impressão?
Escala \(= \dfrac{60}{50}\cdot100\% = \mathbf{120\%}\).
Q7 — Massa de papel usada
Com \(a=5\) cm e papel 180 g/m², estime a massa do papel (sem abas).
Área \(=2\sqrt{3}\,a^2=2\sqrt{3}\cdot25\approx 86{,}6\ \text{cm}^2=8{,}66\times10^{-3}\ \text{m}^2\).
Massa \(\approx 180\cdot 8{,}66\times10^{-3}=\mathbf{1{,}56\ \text{g}}\) (aprox.).
Q8 — Ângulo em um vértice do sólido montado
Após montar o octaedro, quantos triângulos se encontram em cada vértice? Qual a soma dos ângulos ali?
Encontram-se 4 triângulos equiláteros; soma \(=4\cdot60^\circ=240^\circ\) (< 360°), o que dá curvatura positiva — por isso “fecha” no espaço.
Materiais e produtos do blog
Turbine seus estudos com nossos materiais organizados e prontos para impressão/uso:
- Mapas Mentais de Matemática — resumos visuais para revisar conteúdos de forma rápida.
- ENEM Matemática — guia focado no exame, com dicas e listas por competência.
- Pacote com 10 e-books — coleção digital para estudar onde quiser.
- Banco de Questões de Matemática — centenas de exercícios organizados por tema e dificuldade.
- Canais Oficiais de Matemática — indicações confiáveis para acompanhar novidades e revisões.






















