Introdução aos Poliedros
Um poliedro é uma figura geométrica tridimensional formada por um conjunto de faces planas, onde cada face é um polígono. A interseção de duas faces é uma aresta, e o encontro de três ou mais arestas é um vértice. Os poliedros estão presentes em várias áreas da matemática, arquitetura e natureza, e são estudados tanto pela sua estrutura quanto pelas suas propriedades matemáticas.
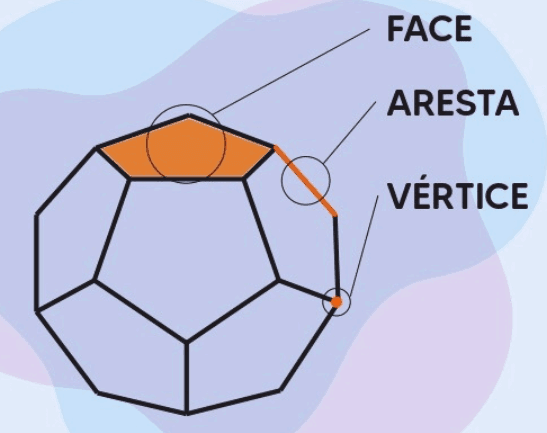
Elementos de um Poliedro
Os principais elementos de um poliedro são:
- F (Face): Cada uma das superfícies planas que formam o poliedro.
- A (Aresta): O segmento de linha onde duas faces se encontram.
- V (Vértice): O ponto onde três ou mais arestas se encontram.
Teorema de Euler
O Teorema de Euler é uma das relações fundamentais na geometria dos poliedros. Para qualquer poliedro convexo, a relação entre o número de faces (F), arestas (A) e vértices (V) é dada por:
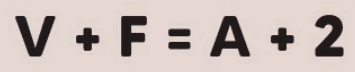
Essa fórmula é conhecida como a Fórmula de Euler e aplica-se a todos os poliedros convexos. Por exemplo, para um cubo, que possui 6 faces, 12 arestas e 8 vértices:
8 – 12 + 6 = 2
O teorema de Euler ajuda a confirmar se uma determinada construção geométrica pode ser considerada um poliedro convexo.
Exemplo 1 : Um cubo possui 6 faces quadradas, 12 arestas e 8 vértices. Verifique a relação dada pelo Teorema de Euler.
Solução: Vamos utilizar a fórmula de Euler:
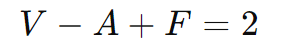
Substituindo os valores conhecidos:
8−12+6=2
O resultado é 2, confirmando que o cubo satisfaz o Teorema de Euler.
Exemplo 2: Um tetraedro tem 4 faces e 4 vértices. Calcule o número de arestas e verifique se o Teorema de Euler é satisfeito.
Solução: Sabemos que o tetraedro tem 4 faces e 4 vértices. Para encontrar o número de arestas, podemos usar o Teorema de Euler:
V−A+F=2
Substituindo V=4 e F=4, temos:
4−A+4=2
Resolvendo para A:
8−A=2 ⟹ A=6
Portanto, o tetraedro tem 6 arestas, e o resultado confirma o Teorema de Euler.
Exemplo 3: Um dodecaedro possui 12 faces e 30 arestas. Determine o número de vértices e verifique se o Teorema de Euler é satisfeito.
Solução: Vamos usar a fórmula de Euler:
V−A+F=2
Substituindo F=12 e A=30, temos:
V−30+12=2
Resolvendo para V:
V−18=2 ⟹ V=20
Portanto, o dodecaedro tem 20 vértices, e o resultado confirma o Teorema de Euler.
Exemplo 4: Um icosaedro possui 20 faces e 12 vértices. Calcule o número de arestas e verifique o Teorema de Euler.
Solução: Sabemos que F=20 e V=12. Usando o Teorema de Euler:
V−A+F=2
Substituindo os valores conhecidos:
12−A+20=2
Resolvendo para A:
32−A=2 ⟹ A=30
Portanto, o icosaedro tem 30 arestas, e o resultado confirma o Teorema de Euler.
Exemplo 5: Um octaedro tem 8 faces e 12 arestas. Determine o número de vértices e verifique a relação de Euler.
Solução: Sabemos que F=8 e A=12. Usando a fórmula de Euler:
V−A+F=2
Substituindo os valores conhecidos:
V−12+8=2
Resolvendo para V:
V−4=2 ⟹ V=6
Portanto, o octaedro tem 6 vértices, e o resultado confirma o Teorema de Euler.
Arestas e Faces
As arestas e faces de um poliedro determinam sua forma e estrutura. Um poliedro pode ser classificado de várias maneiras com base no número e na disposição de suas faces e arestas. Algumas das classificações mais comuns incluem:
- Tetraedro: 4 faces, 6 arestas, 4 vértices.
- Cubo (ou Hexaedro regular): 6 faces, 12 arestas, 8 vértices.
- Octaedro: 8 faces, 12 arestas, 6 vértices.
- Dodecaedro: 12 faces, 30 arestas, 20 vértices.
- Icosaedro: 20 faces, 30 arestas, 12 vértices.

Poliedros de Platão
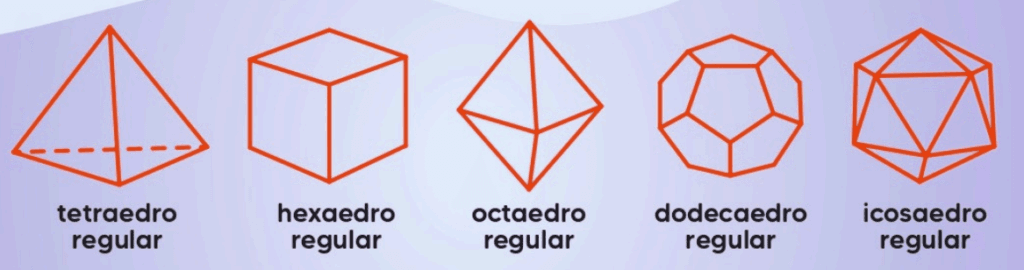
Os poliedros de Platão são um grupo especial de poliedros regulares. Um poliedro é regular se todas as suas faces são polígonos regulares congruentes e o mesmo número de faces se encontra em cada vértice. Existem exatamente cinco poliedros regulares, conhecidos como Poliedros de Platão:
- Tetraedro: Com 4 faces triangulares.
- Cubo (Hexaedro regular): Com 6 faces quadradas.
- Octaedro: Com 8 faces triangulares.
- Dodecaedro: Com 12 faces pentagonais.
- Icosaedro: Com 20 faces triangulares.
Esses poliedros são nomeados em homenagem ao filósofo grego Platão, que associou cada um deles a um dos elementos clássicos: fogo (tetraedro), terra (cubo), ar (octaedro), água (icosaedro) e o éter ou universo (dodecaedro).
Conclusão
Os poliedros são figuras fascinantes tanto por sua simetria quanto pelas relações matemáticas que os definem. O Teorema de Euler oferece uma maneira poderosa de compreender a estrutura dos poliedros convexos, enquanto os Poliedros de Platão representam os exemplos mais simétricos e elegantes dessa classe de formas tridimensionais. Estudar poliedros é mergulhar em um mundo onde a matemática e a geometria se encontram para formar belas e complexas figuras.
Leia também
O Cubo: Propriedades e Fórmulas Essenciais
O Paralelepípedo: Propriedades e Fórmulas Essenciais
Pirâmides: Propriedades, Fórmulas e Aplicações
Tetraedro Regular: Propriedades, Fórmulas e Aplicações
Tronco de Pirâmide: Propriedades, Fórmulas e Proporções
Cilindro: Conceitos e Cálculos
Cone: Tudo o Que Você Precisa Saber
Poliedros: Estrutura, Teorema de Euler e Poliedros de Platão










