Conteúdo: Coordenadas, regiões no plano cartesiano e pontuação
Questão 15. (OBMEP) Manoel testa sua pontaria lançando 5 flechas que atingiram o alvo nos pontos A, B, C, D e E, de coordenadas:
- A = \( (1,\ -1) \)
- B = \( (2{,}5,\ 1) \)
- C = \( (-1,\ 4) \)
- D = \( (-4,\ -4) \)
- E = \( (6,\ 5) \)
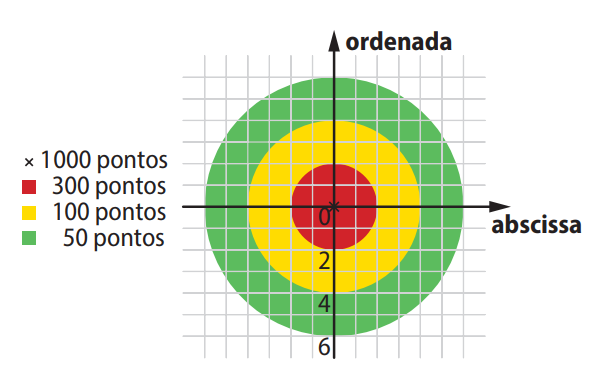
A imagem mostra as regiões de pontuação do alvo. Cada cor representa uma pontuação diferente conforme a distância da origem:
a) Marque os pontos A, B, C, D e E.
b) Quantas flechas ele acertou no interior do
menor círculo?
c) Ao todo, quantos pontos Manoel fez?🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Precisamos determinar a pontuação total de Manoel observando em qual região cada flecha caiu com base nas coordenadas fornecidas e nas regiões circulares do alvo.
1) Determinar a distância de cada ponto até a origem (0, 0):
- A: \( \sqrt{1^2 + (-1)^2} = \sqrt{2} \approx 1{,}41 \) → Região vermelha → 1000 pontos
- B: \( \sqrt{(2{,}5)^2 + 1^2} = \sqrt{6{,}25 + 1} = \sqrt{7{,}25} \approx 2{,}69 \) → Região amarela → 300 pontos
- C: \( \sqrt{(-1)^2 + 4^2} = \sqrt{1 + 16} = \sqrt{17} \approx 4{,}12 \) → Região verde → 50 pontos
- D: \( \sqrt{(-4)^2 + (-4)^2} = \sqrt{16 + 16} = \sqrt{32} \approx 5{,}66 \) → Região verde → 50 pontos
- E: \( \sqrt{6^2 + 5^2} = \sqrt{36 + 25} = \sqrt{61} \approx 7{,}81 \) → Fora do alvo → 0 pontos
2) Contabilizar quantas flechas atingiram o menor círculo:
Somente o ponto A está no círculo vermelho (menor círculo).
Resposta (b): 1 flecha
3) Somar a pontuação total:
\( 1000 + 300 + 50 + 50 + 0 = 1400 \) pontos
Resposta (c): 1400 pontos
✅ Conclusão:
- b) 1 flecha no menor círculo
- c) Total de pontos: $$ \boxed{1400} $$
