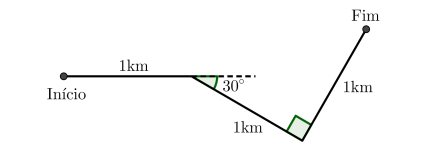
Uma pessoa anda 1 km em linha reta, depois gira \(30^\circ\) à sua direita e anda mais 1 km. Por fim, gira \(90^\circ\) à sua esquerda e anda mais 1 km. Qual a distância, em km, entre os pontos inicial e final desse deslocamento?
(A) \(\sqrt{4+\sqrt{3}}\)
(B) \(\sqrt{4+2\sqrt{3}}\)
(C) \(1+\sqrt{2}\)
(D) \(\sqrt{11+2\sqrt{3}}\)
(E) \(\frac{7}{\sqrt{2}}\)
Solução passo a passo:
Considerando a decomposição em triângulos retângulos e aplicando trigonometria:
- O deslocamento forma triângulos retângulos com ângulos de \(30^\circ\) e \(90^\circ\).
- Usamos seno e cosseno para decompor os deslocamentos em \(x\) e \(y\).
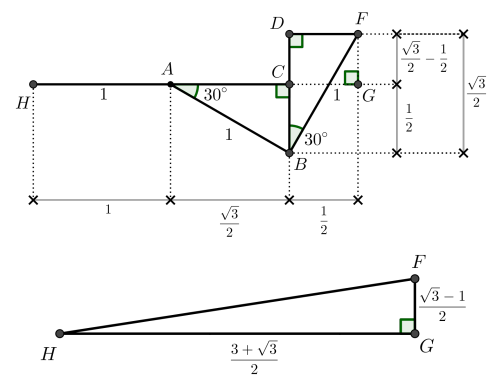
O deslocamento total em \(x\) e \(y\) é: \[ x = 1 + \cos 30^\circ = 1 + \frac{\sqrt{3}}{2}, \quad y = 1 – \frac{1}{2} = \frac{1}{2} \]
Calculando a distância pelo Teorema de Pitágoras:
\[ d = \sqrt{x^2 + y^2} = \sqrt{\left(1+\frac{\sqrt{3}}{2}\right)^2 + \left(\frac{1}{2}\right)^2} = \sqrt{4 + \sqrt{3}} \]
Resposta: (A) \(\sqrt{4+\sqrt{3}}\)
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
