Sabendo que o lado menor do paralelogramo preto corresponde a \( \frac{1}{4} \) do comprimento do lado do hexágono regular na figura abaixo, qual fração da área do hexágono corresponde à área do paralelogramo preto?

(A) \( \frac{1}{16} \)
(B) \( \frac{1}{9} \)
(C) \( \frac{1}{8} \)
(D) \( \frac{1}{6} \)
(E) \( \frac{1}{4} \)
Ver solução passo a passo
Resposta correta: (D)
Dividindo o hexágono regular \(ABCDEF\) pelas suas diagonais que passam pelo centro, obtemos **6 triângulos equiláteros congruentes**.
Se traçarmos as diagonais \(AE\) e \(BD\), e também o segmento que liga os pontos médios de \(AB\) e \(DE\), cada triângulo equilátero é dividido em dois triângulos retângulos menores, totalizando **12 triângulos retângulos congruentes**.
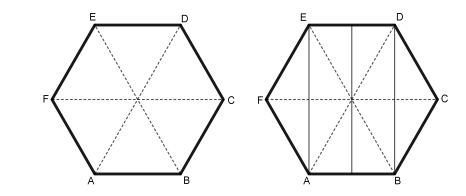
O retângulo \(ABDE\) é formado por 8 desses triângulos, o que equivale a:
\[ \frac{2}{3} \text{ da área do hexágono.} \]
O paralelogramo preto tem **1/4 da base** do retângulo \(ABDE\) e **a mesma altura**. Logo, sua área é:
\[ \frac{1}{4} \times \frac{2}{3} = \frac{1}{6} \text{ da área do hexágono.} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!





























