PROFMAT 2021 – Questão 12 | Geometria Plana – Área e Medianas
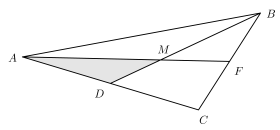
Na figura abaixo, o ponto \(M\) é a interseção das medianas \(BD\) e \(AF\). Se a área do triângulo \(ABC\) é igual a 1, a área do triângulo \(ADM\) é:
(A) \( \frac{1}{6} \)
(B) \( \frac{2}{3} \)
(C) \( \frac{1}{4} \)
(D) \( \frac{1}{2} \)
(E) \( \frac{1}{3} \)
Ver solução passo a passo
Resposta correta: (A)
As medianas de um triângulo dividem-no em 6 triângulos de **áreas iguais**. Sendo a área total do triângulo \(ABC = 1\), cada pequeno triângulo formado pelas medianas possui área:
\[ \frac{1}{6} \]
O triângulo \(ADM\) é composto exatamente por **um desses 6 triângulos**. Logo, sua área é:
\[ \text{Área}(ADM) = \frac{1}{6} \]
✅ Confira nossos Mapas Mentais de Matemática
📘 E baixe os 10 eBooks de Matemática para reforçar seus estudos!
📘 E baixe os 10 eBooks de Matemática para reforçar seus estudos!