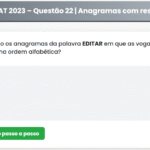
Em um terreno retangular de \(1360\,\text{m}^2\) de área será construída uma casa térrea de \(480\,\text{m}^2\), conforme as dimensões indicadas na figura. Nessas condições, um valor possível para as dimensões do terreno será:
(A) 85 m × 16 m
(B) 80 m × 17 m
(C) 68 m × 10 m
(D) 40 m × 34 m
(E) 34 m × 20 m
Ver solução passo a passo
Resposta correta: (D)
Seja a casa um retângulo de dimensões \(x\) por \(y\), com área:
\[ xy = 480 \]
O terreno acrescenta **10 m** de cada lado no comprimento e **5 m** de cada lado na largura, resultando em dimensões \(x + 20\) e \(y + 10\). Logo, a área do terreno é:
\[ (x + 20)(y + 10) = 1360 \]
Expandindo:
\[ xy + 10x + 20y + 200 = 1360 \]
Substituindo \(xy = 480\):
\[ 480 + 10x + 20y + 200 = 1360 \implies 10x + 20y = 680 \]
Dividindo por 10:
\[ x + 2y = 68 \]
Agora temos o sistema:
\[ \begin{cases} xy = 480 \\ x + 2y = 68 \end{cases} \]
Substituindo \(x = 68 – 2y\) na primeira equação:
\[ (68 – 2y)y = 480 \implies 68y – 2y^2 = 480 \]
Reorganizando:
\[ 2y^2 – 68y + 480 = 0 \implies y^2 – 34y + 240 = 0 \]
Resolvendo a equação, obtemos \(y = 10\) ou \(y = 24\). Portanto, os pares \((x, y)\) são \((48, 10)\) e \((20, 24)\).
Assim, os terrenos possíveis têm dimensões:
- 68 m × 20 m
- 40 m × 34 m ✅
Logo, uma possível dimensão do terreno é **40 m × 34 m**.
📘 E baixe os 10 eBooks de Matemática para reforçar seus estudos!
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Preparação para o PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade