PROFMAT 2021 – Questão 24 | Círculos Concêntricos
Os dois círculos da figura abaixo são concêntricos e \( AB \) é uma corda do círculo de maior raio e tangente ao círculo de menor raio. Se o raio do círculo maior é 13 cm e \( AB = 24 \) cm, o raio do círculo menor, em centímetros, é:
Ver solução passo a passo
Resposta correta: (B) 5
Seja \( C \) o centro dos círculos e \( D \) o ponto de tangência. O triângulo \( ACD \) é retângulo em \( D \), com hipotenusa de 13 cm (raio maior) e cateto horizontal \( AD \) que é metade da corda \( AB \), ou seja, 12 cm.
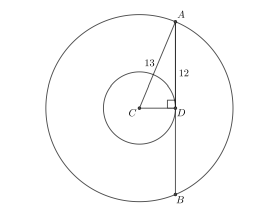
Aplicando o Teorema de Pitágoras no triângulo \( ACD \): \[ 13^2 = 12^2 + r^2 \quad \Rightarrow \quad r^2 = 169 – 144 = 25 \] Portanto: \[ r = 5 \text{ cm.} \]
✅ Reforce este tema com os Mapas Mentais de Geometria
📘 E baixe nossos 10 eBooks gratuitos para revisar rapidamente.
