Para medir a altura de um edifício vertical, um engenheiro instalou um teodolito a uma altura de \(1{,}70 \, m\) do solo, observando seu topo sob um ângulo de \(43^\circ\), a partir da horizontal que passa pelo teodolito. Sabendo que o teodolito está a \(80\, m\) do edifício, determine a altura do edifício em metros. Considere: \(\sin 43^\circ = 0{,}682\), \(\cos 43^\circ = 0{,}731\) e \(\tan 43^\circ = 0{,}933\).
(A) 69,92
(B) 76,34
(C) 84,8
(D) 93,3
(E) 95
Ver solução passo a passo
Resposta correta: (B) 76,34
Aplicando a razão trigonométrica tangente no triângulo retângulo formado: \[ \tan 43^\circ = \frac{x}{80} = 0{,}933 \] \[ x = 80 \times 0{,}933 = 74{,}64\,m \]
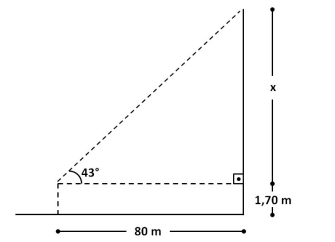
Somando a altura do teodolito (\(1{,}70\,m\)), a altura do edifício será: \[ 74{,}64 + 1{,}70 = 76{,}34\,m \]
✅ Portanto, a altura do edifício é 76,34 m.
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Preparação para o PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade




























