Considere um trapézio cuja base maior mede \(a\), a base menor mede \(b\) e cujos lados não paralelos medem \(c\) e \(d\). Qual das combinações abaixo não é possível?
(A) \(a = 3, b = 1, c = 2, d = 2\)
(B) \(a = 4, b = 2, c = 2, d = 2\)
(C) \(a = 4, b = 1, c = 2, d = 1\)
(D) \(a = 4, b = 1, c = 1, d = 2\)
(E) \(a = 4, b = 2, c = 2, d = 2\)
Ver solução passo a passo
Resposta correta: (C)
Considere o trapézio \(ABCD\) com \(AB = b\), \(CD = a\), \(AD = c\) e \(BC = d\). Traçamos \(DE\) paralelo a \(BC\), formando o paralelogramo \(BECD\), de modo que \(DE = d\).
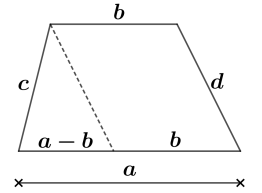
Para o triângulo \(ABE\) existir, as desigualdades devem ser satisfeitas:
\[ b + c > d,\quad b + d > c, \quad c + d > b \]
Substituindo os valores de cada alternativa:
- (A) \(a = 3, b = 1, c = 2, d = 2\) → Todas as desigualdades são verdadeiras.
- (B) \(a = 4, b = 2, c = 2, d = 2\) → Todas as desigualdades são verdadeiras.
- (C) \(a = 4, b = 1, c = 2, d = 1\) → Uma desigualdade falha → impossível.
- (D) \(a = 4, b = 1, c = 1, d = 2\) → Todas as desigualdades são verdadeiras.
- (E) \(a = 4, b = 2, c = 2, d = 2\) → Todas as desigualdades são verdadeiras.
Logo, a alternativa (C) não é possível.
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!