PROFMAT 2021 – Questão 5 | Geometria Plana e Teorema de Pitágoras
Sobre um segmento \(AB\) são construídos dois quadrados adjacentes com lados de medidas \(x\) e \(y\), conforme a figura. Podemos afirmar que a medida do segmento \(CD\), em função de \(x\) e \(y\), é:
Ver solução passo a passo
Resposta correta: (A)
Prolongamos o lado superior do quadrado menor até que ele intersecte o segmento \(AC\) no ponto \(E\), obtendo o triângulo retângulo \(CDE\) de hipotenusa \(CD\) e catetos:
- \(x+y\)
- \(x-y\)
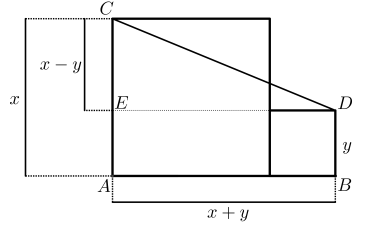
Aplicando o Teorema de Pitágoras:
\[ CD = \sqrt{(x+y)^2 + (x-y)^2} \] \[ = \sqrt{x^2 + 2xy + y^2 + x^2 – 2xy + y^2} \] \[ = \sqrt{2x^2 + 2y^2} = \sqrt{2(x^2 + y^2)} \]
✅ Aprenda mais com nossos Mapas Mentais de Matemática
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!
