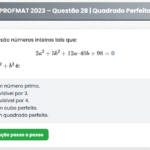
A diagonal menor do losango de lado \( \ell \) e com dois ângulos internos medindo \(30^\circ\) é igual a:
(A) \( \ell \sqrt{2 – \sqrt{3}} \)
(B) \( \ell \sqrt{3 + \sqrt{3}} \)
(C) \( \ell \sqrt{2 – \sqrt{2}} \)
(D) \( \ell \sqrt{2 + \sqrt{2}} \)
(E) \( \ell \sqrt{2 + \sqrt{3}} \)
Ver solução passo a passo
Resposta correta: (A)
1. **Identificação da diagonal menor** A menor diagonal é **oposta ao menor ângulo** de \(30^\circ\). Aplicando a **Lei dos Cossenos**, temos:
\[ d^2 = \ell^2 + \ell^2 – 2 \ell^2 \cos 30^\circ \]
2. **Substituindo o valor do cosseno** \[ \cos 30^\circ = \frac{\sqrt{3}}{2} \] \[ d^2 = 2\ell^2 \left(1 – \frac{\sqrt{3}}{2}\right) = \ell^2 \left(2 – \sqrt{3}\right) \]
3. **Resultado final** \[ d = \ell \sqrt{2 – \sqrt{3}} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!