Introdução
A Progressão Aritmética (PA) é uma sequência de números na qual cada termo, a partir do segundo, é obtido pela soma do termo anterior com uma constante chamada de razão. As PA’s são amplamente utilizadas em diversas áreas, como finanças, física e economia, devido à sua simplicidade e aplicação prática. Elas permitem o estudo de padrões numéricos e a análise de crescimento ou decrescimento linear em diversos contextos.
Termo Geral
O termo geral de uma Progressão Aritmética é uma expressão que permite calcular qualquer termo da sequência a partir de sua posição (n). Dado o primeiro termo a1 e a razão r, o termo geral an pode ser expresso pela fórmula:
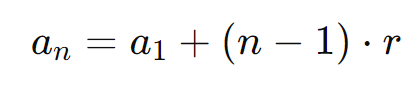
Onde:
- ( an ) é o n-ésimo termo da PA,
- ( a1 ) é o primeiro termo da PA,
- ( r ) é a razão da PA,
- ( n ) é a posição do termo na sequência.
Essa fórmula é essencial para determinar qualquer termo sem a necessidade de calcular todos os anteriores, economizando tempo e esforço.
Exemplo:
Considere a PA onde a1 = 5 e r = 3. Para encontrar o 10º termo a10:
a10 = 5 + (10-1) . 3 = 5 + 9 . 3 = 5 + 27 = 32
Razão
A razão ( r ) é a constante que é somada ao termo anterior para obter o próximo termo da sequência. Ela pode ser positiva, negativa ou zero. A razão determina o comportamento da PA:
- ( r > 0 ): A sequência é crescente.
- ( r < 0 ): A sequência é decrescente.
- ( r = 0 ): A sequência é constante, ou seja, todos os termos são iguais.
A razão pode ser calculada pela diferença entre qualquer termo e o termo anterior:
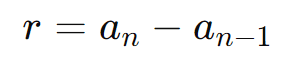
Exemplo:
Seja uma PA com ( a1 = 7 ) e ( a2 = 10 ). A razão ( r ) é:
r = 10 – 7 = 3
Termo Médio
Em uma Progressão Aritmética, o termo médio entre dois termos ( ai ) e ( aj ) é simplesmente a média aritmética desses termos. Se ( ak ) é o termo médio entre ( ai ) e ( aj ), então:
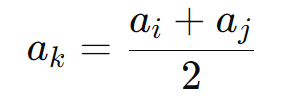
Essa propriedade é especialmente útil para verificar se uma sequência é uma PA ou para encontrar um termo intermediário.
Exemplo:
Considere a PA ( 2, 5, 8, 11, 14 ). O termo médio entre ( a1 = 2 ) e ( a3 = 8 ) é:
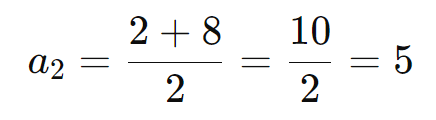
Soma dos Termos
A soma dos n primeiros termos de uma Progressão Aritmética é dada pela fórmula:
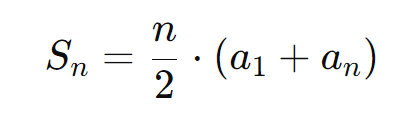
Onde:
- ( Sn ) é a soma dos n primeiros termos,
- ( n ) é o número de termos,
- ( a1 ) é o primeiro termo,
- ( an ) é o n-ésimo termo.
Alternativamente, a soma pode ser calculada usando a razão ( r ):

Essa fórmula é especialmente útil para calcular rapidamente a soma de uma grande quantidade de termos sem precisar somar cada um individualmente.
Exemplo:
Calcule a soma dos 10 primeiros termos da PA onde ( a1 = 5 ) e ( r = 3 ):
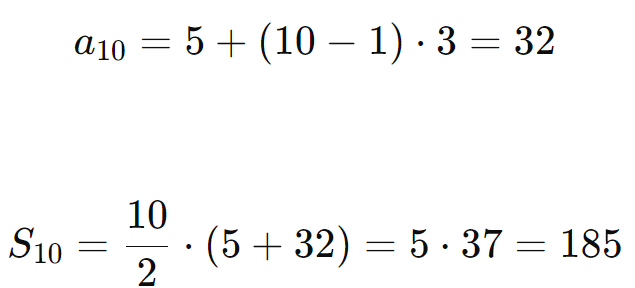
Conclusão
A Progressão Aritmética é uma ferramenta poderosa e fundamental na matemática. Compreender seu termo geral, razão, termo médio e soma permite resolver uma vasta gama de problemas. Seja em análise de padrões ou em aplicações práticas, a PA desempenha um papel essencial no estudo de sequências numéricas e em várias disciplinas científicas.
Leia também
Questões de Progressão Aritmética
- Dada a PA: 3,7,11,15,… Qual é o 10º termo dessa sequência?
a) 31
b) 35
c) 39
d) 43 - Se o primeiro termo de uma PA é 5 e a razão é 8, qual é o valor do 7º termo?
a) 45
b) 53
c) 61
d) 69 - Em uma PA, o 4º termo é 18 e o 9º termo é 33. Qual é a razão dessa progressão?
a) 2
b) 3
c) 4
d) 5 - Determine a soma dos 20 primeiros termos de uma PA onde a1=10 e r=5.
a) 1100
b) 1200
c) 1300
d) 1400 - Em uma PA, o 3º termo é 14 e o 7º termo é 26. Qual é a soma dos 12 primeiros termos?
a) 192
b) 204
c) 216
d) 228 - Dada a PA: 6,14,22,30,… qual é o 15º termo?
a) 98
b) 102
c) 106
d) 110 - Se o 2º termo de uma PA é 12 e o 5º termo é 24, qual é o 8º termo?
a) 36
b) 38
c) 40
d) 42 - Calcule a soma dos 25 primeiros termos de uma PA onde a1=7 e r=3.
a) 925
b) 950
c) 975
d) 1000 - Em uma PA, o 1º termo é 2 e o 10º termo é 38. Qual é o valor do 15º termo?
a) 58
b) 62
c) 66
d) 70 - Se o 6º termo de uma PA é 27 e o 11º termo é 42, qual é a soma dos 15 primeiros termos?
a) 345
b) 360
c) 375
d) 390
Gabarito
- c
- c
- b
- d
- c
- b
- c
- c
- c
- c