Quadrantes da Circunferência Trigonométrica
A circunferência trigonométrica pode ser dividida em quatro quadrantes, cada um deles representando uma região do plano cartesiano. Em cada quadrante, as funções trigonométricas seno, cosseno e tangente apresentam sinais específicos que ajudam a resolver cálculos de ângulos e identificar coordenadas.
Representação dos Quadrantes
Na imagem abaixo, temos a divisão da circunferência trigonométrica em graus e em radianos:
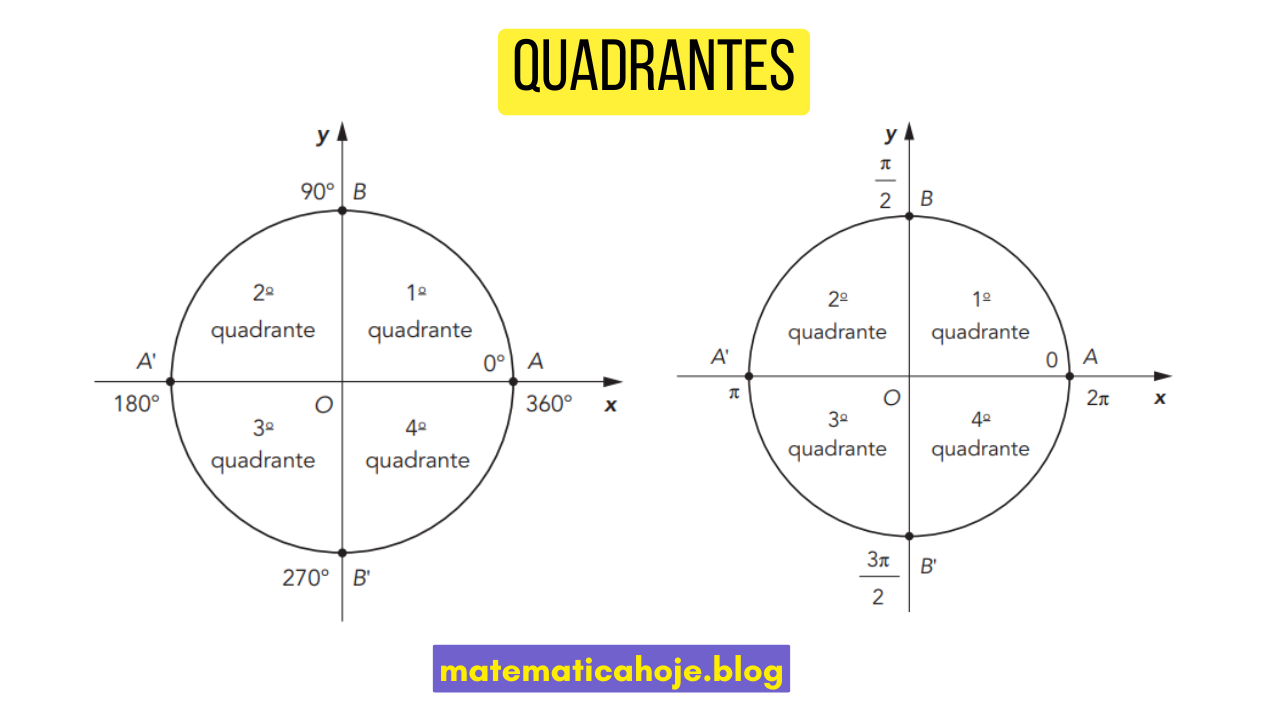
- 1º Quadrante: de \(0^\circ\) a \(90^\circ\) (ou de \(0\) a \(\frac{\pi}{2}\)).
- 2º Quadrante: de \(90^\circ\) a \(180^\circ\) (ou de \(\frac{\pi}{2}\) a \(\pi\)).
- 3º Quadrante: de \(180^\circ\) a \(270^\circ\) (ou de \(\pi\) a \(\frac{3\pi}{2}\)).
- 4º Quadrante: de \(270^\circ\) a \(360^\circ\) (ou de \(\frac{3\pi}{2}\) a \(2\pi\)).
Sinais das Funções Trigonométricas
Os sinais de seno, cosseno e tangente variam conforme o quadrante:
| Quadrante | Seno | Cosseno | Tangente |
|---|---|---|---|
| 1º Quadrante | + | + | + |
| 2º Quadrante | + | – | – |
| 3º Quadrante | – | – | + |
| 4º Quadrante | – | + | – |
Exemplo Resolvido
Exemplo:
Determine o sinal do seno, cosseno e tangente para o ângulo de \(210^\circ\).
Solução: O ângulo \(210^\circ\) está no 3º quadrante. Assim:
- \(\sin 210^\circ < 0\)
- \(\cos 210^\circ < 0\)
- \(\tan 210^\circ > 0\)
📘 Exercícios de múltipla escolha
1) Em qual quadrante está o ângulo de \(135^\circ\)?
- 1º Quadrante
- 2º Quadrante
- 3º Quadrante
- 4º Quadrante
Ver solução
O ângulo de \(135^\circ\) pertence ao intervalo \((90^\circ,180^\circ)\), ou seja, está no 2º Quadrante.
2) O ângulo de \(300^\circ\) apresenta quais sinais para seno, cosseno e tangente?
- \(\sin > 0, \cos > 0, \tan > 0\)
- \(\sin > 0, \cos < 0, \tan < 0\)
- \(\sin < 0, \cos > 0, \tan < 0\)
- \(\sin < 0, \cos < 0, \tan > 0\)
Ver solução
O ângulo \(300^\circ\) pertence ao 4º Quadrante: \(\sin < 0\), \(\cos > 0\), \(\tan < 0\).
Links Relacionados
📚 Continue estudando
Os quadrantes da circunferência trigonométrica são fundamentais para determinar o sinal das funções trigonométricas em diferentes ângulos.






















