Questão 12
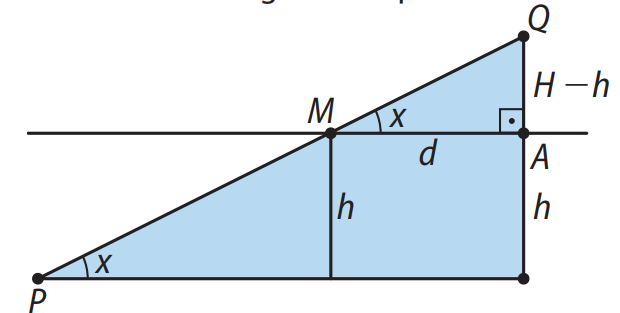
Enunciado: (UECE) Um cabo de aço, medindo \(c\) metros de comprimento, é estendido em linha reta fixado em três pontos, a saber: \(P\) e \(Q\) em seus extremos e \(M\) em um ponto intermediário. O ponto \(P\) está localizado no solo plano horizontal e os pontos \(M\) e \(Q\) estão localizados no alto de duas torres erguidas verticalmente no mesmo solo. As medidas, em metros, das alturas das torres e a distância entre elas são, respectivamente, \(h\), \(H\) e \(d\). Se \(x\) é a medida em graus do ângulo que o cabo faz com o solo, a diferença entre a altura da torre maior e a da menor é:
Alternativas:
- a) \( c \cdot tg (x) \)
- b) \( d \cdot tg (x) \)
- c) \( \frac{c \cdot h}{H} tg (x) \)
- d) \( \frac{d \cdot h}{H} tg (x) \)
