Questão 2 – Razões e Proporções

Questão 2

Solução Passo a Passo:

Vamos usar a semelhança dos triângulos formados pela pessoa e pelo poste com suas respectivas sombras.

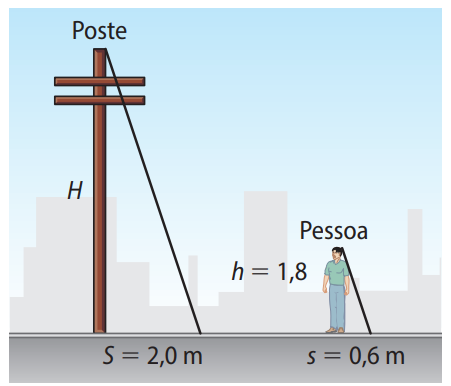
Altura da pessoa: \( h = 1{,}8 \, \text{m} \)
Sombra da pessoa: \( s = 0{,}6 \, \text{m} \)
Sombra do poste: \( S = 2{,}0 \, \text{m} \)

Vamos determinar a altura do poste \( H \), usando a proporção:

\[ \frac{H}{S} = \frac{h}{s} \] \[ \frac{H}{2{,}0} = \frac{1{,}8}{0{,}6} \] \[ \frac{H}{2{,}0} = 3 \Rightarrow H = 3 \cdot 2{,}0 = 6{,}0 \, \text{m} \]

Agora que sabemos que o poste tem 6,0 m de altura, vamos calcular o novo comprimento da sombra da pessoa quando a sombra do poste diminui 50 cm:

Nova sombra do poste: \( S’ = 2{,}0 – 0{,}5 = 1{,}5 \, \text{m} \)

Usamos novamente a razão da semelhança:

\[ \frac{H}{S’} = \frac{h}{s’} \] \[ \frac{6{,}0}{1{,}5} = \frac{1{,}8}{s’} \] \[ 4 = \frac{1{,}8}{s’} \Rightarrow s’ = \frac{1{,}8}{4} = 0{,}45 \, \text{m} = \boxed{45\,\text{cm}} \]

Resposta correta: letra b.

📌 Aproveite também:

• 🧠 Mapas Mentais de Matemática
• 📘 10 eBooks de Matemática para Provas e Concursos

📚 Continue aprendendo!

✅ Confira a lista completa com 11 questões resolvidas de Matemática com gráficos e solução visual passo a passo:
👉 Acesse a lista completa de exercícios

📐 Aprofunde-se no conteúdo com o artigo completo sobre Relações Métricas no Triângulo Retângulo:
🔍 Leia o artigo completo agora