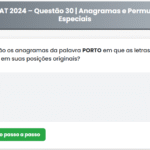
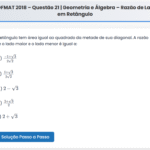
Questão 20 – PROFMAT 2025
Os números de três algarismos \(M = abc\) e \(N = cba\) estão escritos em ordem invertida.
Sabendo que \(a > 4\) e que \(M – N = 198\), quantos são os possíveis valores de \(M\)?
(A) 20
(B) 30
(C) 40
(D) 50
(E) 60
Solução Passo a Passo
1º Passo: Expresse \(M – N\) em função de \(a, b, c\):
\[ M – N = 100a + 10b + c – (100c + 10b + a) = 99(a-c) \]
Sabemos que \(M – N = 198\), então:
\[ 99(a-c) = 198 \implies a-c = 2 \]
2º Passo: Como \(a > 4\), temos \(a = 5,6,7,8,9\) e \(c = a-2 = 3,4,5,6,7\).
3º Passo: O algarismo \(b\) pode variar de 0 a 9 (10 possibilidades).
4º Passo: Total de valores possíveis de \(M\):
\[ 5 \times 10 = 50 \]
Resposta: Alternativa D.
📚 Coleção: A Matemática do Ensino Médio
A Matemática do Ensino Médio – Volume 1
👉 Comprar Agora
A Matemática do Ensino Médio – Volume 2
👉 Comprar Agora
A Matemática do Ensino Médio – Volume 3
👉 Comprar Agora
