Questão 4 – Seno, Cosseno e Tangente

Questão 4

Enunciado: Em um triângulo retângulo, um cateto mede 15 cm, e a hipotenusa, 17 cm. Calcule o seno, o cosseno e a tangente do maior ângulo agudo desse triângulo.

Solução Passo a Passo:

Primeiro, determinamos o outro cateto utilizando o Teorema de Pitágoras:

\(17^2 = x^2 + 15^2 \Rightarrow x^2 = 289 – 225 = 64 \Rightarrow x = 8 \, \text{cm}\)

Como 8 cm é o menor lado, o ângulo oposto a este cateto é o menor ângulo. Portanto, o maior ângulo agudo está oposto ao cateto de 15 cm.

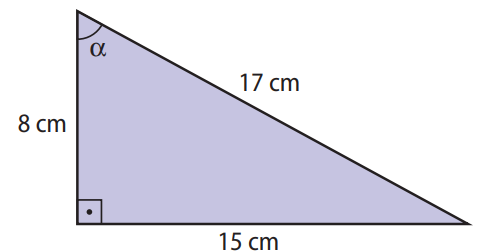
Questão 4 - Triângulo Retângulo

Assim, aplicando as definições de seno, cosseno e tangente, temos:

\(sen \alpha = \frac{15}{17}, \quad \cos \alpha = \frac{8}{17}, \quad tg \alpha = \frac{15}{8}\)

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Relacionadas

Matemática para Concursos: Geometria Plana – Banca VUNESP - Nível Superior

Matemática IBFC 2024: Geometria Plana – Questão Comentada

Geometria Plana – Concurso Joinville 2024 – Banca CESPE

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube
Rolar para cima