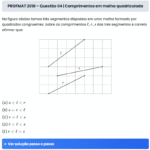
PROFMAT 2025 – Questão 5 | Triângulo Retângulo
Um dos catetos de um triângulo retângulo mede \( \ell \) cm e o ângulo oposto a este cateto mede \( 30^\circ \). Qual a área, em cm², deste triângulo?
(A) \( \frac{\ell^2 \sqrt{3}}{2} \)
(B) \( \frac{\ell^2 \sqrt{3}}{6} \)
(C) \( \frac{\ell^2 \sqrt{3}}{4} \)
(D) \( \frac{\ell^2 \sqrt{3}}{9} \)
(E) \( \frac{\ell^2 \sqrt{3}}{3} \)
(B) \( \frac{\ell^2 \sqrt{3}}{6} \)
(C) \( \frac{\ell^2 \sqrt{3}}{4} \)
(D) \( \frac{\ell^2 \sqrt{3}}{9} \)
(E) \( \frac{\ell^2 \sqrt{3}}{3} \)
Resposta correta: (A)
1º Passo: Em um triângulo 30°-60°-90°: – O cateto oposto a 30° mede \( \ell \); – O cateto oposto a 60° mede \( \ell \sqrt{3} \).
2º Passo: A área de um triângulo retângulo é: \[ A = \frac{\text{cateto}_1 \cdot \text{cateto}_2}{2} \]
3º Passo: Substituindo os catetos: \[ A = \frac{\ell \cdot \ell \sqrt{3}}{2} = \frac{\ell^2 \sqrt{3}}{2} \]
✅ Portanto, a área é \( \frac{\ell^2 \sqrt{3}}{2} \).
🔗 Continue seus estudos: