Confira a resolução detalhada de uma questão típica da banca VUNESP. Entenda o método e prepare-se para suas provas com confiança.
(Banca VUNESP – Nível Médio – 2023 – Diagramas de Venn) Três conjuntos: I, II e III formam um diagrama lógico com a seguinte disposição:
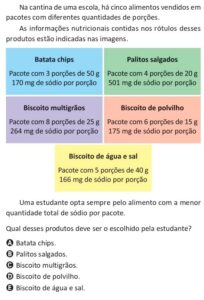
As regiões A, D e E são regiões do conjunto I. As regiões B, E e F são regiões do conjunto II. As regiões C, D e F são regiões do conjunto III. As letras representam o número de elementos da região na qual a letra está inserida. A intersecção simultânea dos três conjuntos não possui elementos. A união dos três conjuntos possui 55 elementos, e sabe-se que:
A + B = 23
A + C = 26
B + C = 25
A região D tem um elemento a mais que a região E, que, por sua vez, tem um elemento a mais que a região F. Sendo assim, é correto afirmar que o conjunto que tem mais elementos supera o conjunto com o menor número de elementos em
A) 2 elementos.
B) 3 elementos.
C) 4 elementos.
D) 1 elemento.
E) 5 elementos.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Diagramas de Venn – VUNESP – Nível Fundamental
Entendendo o Enunciado
Temos três conjuntos I, II e III, representados em um diagrama de Venn, e as seguintes informações:
- A + B = 23
- A + C = 26
- B + C = 25
- A interseção simultânea dos três conjuntos (E ∩ F ∩ D) não possui elementos.
- As regiões D, E e F seguem a relação:
- D = E + 1
- E = F + 1
- A união dos três conjuntos possui 55 elementos.
O objetivo é determinar a diferença entre o conjunto com mais elementos e o conjunto com menos elementos.
O enunciado apresentou as seguintes equações:
(1) A + B = 23 -> B = 23 – A
(2) A + C = 26 -> C = 26 – A
(3) B + C = 25
Substituindo (1) e (2) em (3), temos:
(23 – A) + (26 – A) = 25
49 – 2A = 25
2A = 24
A = 12
Logo:
B = 23 – A = 23 – 12 = 11
C = 26 – A = 26 – 12 = 14
A união dos três conjuntos possui 55 elementos e a região D tem um elemento a mais que a região E, que, por sua vez, tem um elemento a mais que a região F. Então:
(4) A + B + C + D + E + F = 55
(5) D = E + 1
(6) E = F + 1 -> F = E – 1
Substituindo os valores de A, B e C encontrados anteriormente, e as equações (5) e (6) em (4):
12 + 11 + 14 + (E + 1) + E + (E – 1) = 55
3E + 37 = 55
3E = 18
E = 6
Logo:
D = E + 1 = 6 + 1 = 7
F = E – 1 = 6 – 1 = 5
Conjunto I: A + D + E = 12 + 7 + 6 = 25
Conjunto II: B + E + F = 11 + 6 + 5 = 22
Conjunto III: C + D + F = 14 + 7 + 5 = 26
Então, o conjunto que tem mais elementos (26) supera o conjunto com o menor número de elementos (22) em 4 elementos.
RESPOSTA: alternativa C
Gostou desta questão? Confira outras questões resolvidas de Raciocínio Lógico VUNESP aqui.
👉Entre no nosso canal do WhatsApp
[/toggle]
Raciocínio Lógico Lista em PDF Vunesp
🟣Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Médio)
🟢Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Superior)
Questões Vunesp – Matemática PDF: Prepare-se com Qualidade
🟡Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Fundamental
🔵Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Médio
🟠Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Superior
🟢Mapas Mentais de Matemática para Concurso
👉Curso Gratuito de Raciocínio Lógico para Concursos