Razão e Proporção: guia completo com exemplos e exercícios resolvidos
Razão e proporção aparecem em regra de três, porcentagem, escalas, receitas, velocidades e em inúmeras questões de prova. Aqui você aprende do zero, com muitos exemplos e exercícios.
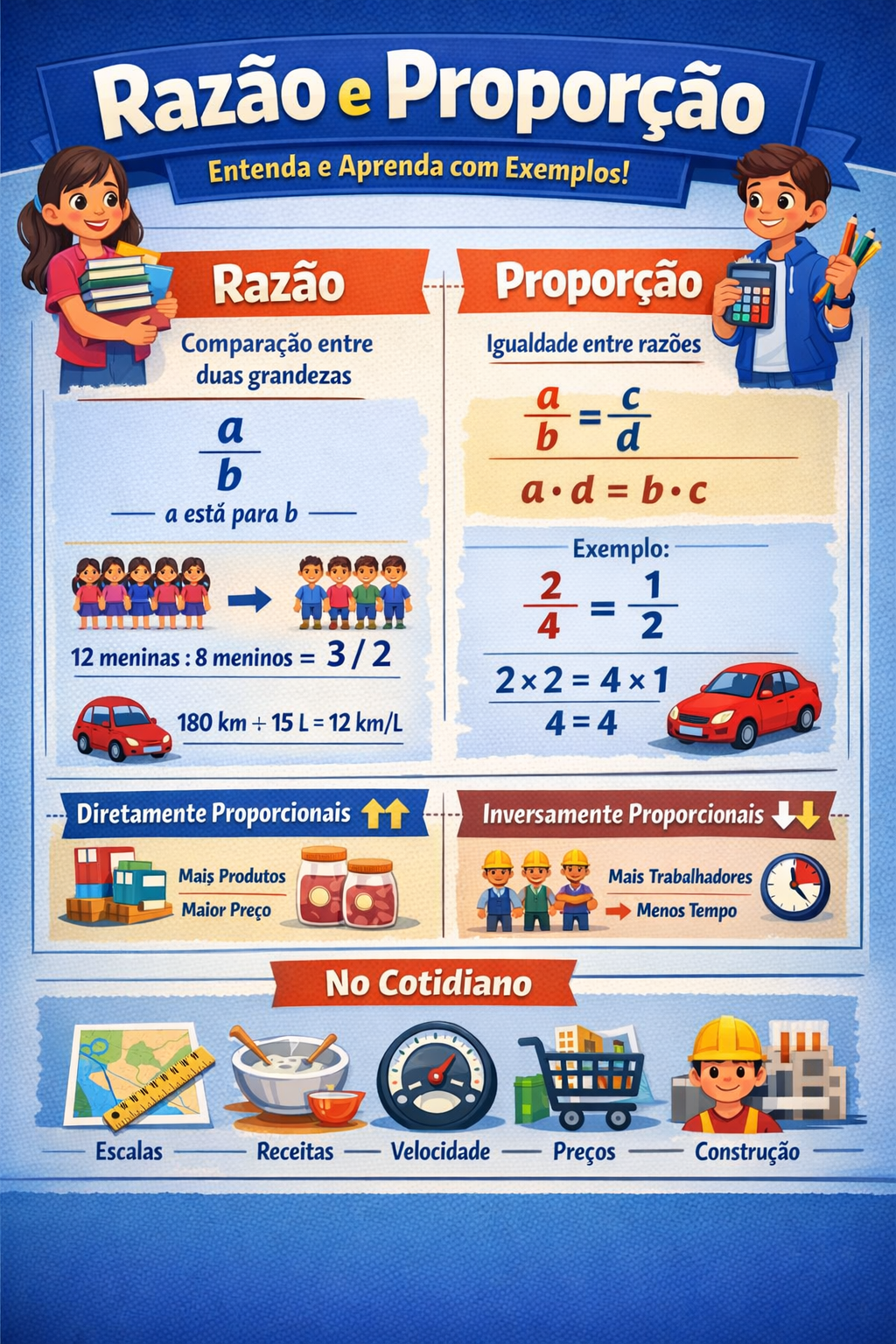
O que é Razão?
A razão é uma forma de comparar duas grandezas por meio de uma divisão. Ela responde perguntas como: “quanto tem de uma coisa em relação à outra?”.
Exemplos simples de razão
Em uma sala há 12 meninas e 8 meninos. Qual a razão entre meninas e meninos?
Ver solução abre/fecha
- Razão (meninas/meninos): \( \frac{12}{8} \).
- Simplificando: \( \frac{12}{8} = \frac{3}{2} \).
Um carro percorre 180 km com 15 litros. Qual a razão km/L?
Ver solução abre/fecha
- Razão (distância/combustível): \( \frac{180}{15} \).
- Calculando: \( \frac{180}{15} = 12 \).
Razão entre grandezas da mesma espécie e de espécies diferentes
Mesma espécie (mesma unidade)
Quando comparamos grandezas com a mesma unidade, a razão é um número puro.
Espécies diferentes (unidades diferentes)
Quando as unidades são diferentes, a razão geralmente tem unidade (ex.: velocidade, densidade, preço por kg).
O que é Proporção?
A proporção é a igualdade entre duas razões. Em linguagem de prova: “duas frações equivalentes”.
Termos da proporção
Na proporção \( \frac{a}{b} = \frac{c}{d} \), chamamos:
- a e d: extremos
- b e c: meios
Verifique se \( \frac{2}{4} \) e \( \frac{1}{2} \) formam uma proporção.
Ver solução abre/fecha
- Multiplicando cruzado: \(2 \cdot 2\) e \(4 \cdot 1\).
- \(2 \cdot 2 = 4\) e \(4 \cdot 1 = 4\).
Proporção direta e proporção inversa
Diretamente proporcionais
Duas grandezas são diretamente proporcionais quando: aumenta com aumenta e diminui com diminui.
Inversamente proporcionais
Duas grandezas são inversamente proporcionais quando: uma aumenta enquanto a outra diminui.
Se 2 kg custam R$ 18, quanto custam 5 kg (preço por kg constante)?
Ver solução abre/fecha
- Montando a proporção: \( \frac{2}{5} = \frac{18}{x} \).
- Multiplicando cruzado: \(2x = 90\).
- Logo: \(x = 45\).
4 trabalhadores fazem uma tarefa em 12 dias. Em quantos dias 6 trabalhadores fariam a mesma tarefa?
Ver solução abre/fecha
- Grandezas inversas: trabalhadores ↑, tempo ↓.
- Produto constante: \(4 \cdot 12 = 6 \cdot x\).
- \(48 = 6x\) → \(x = 8\).
Razão, Proporção e Regra de Três
A regra de três é uma aplicação direta de proporções. Em muitos exercícios, você só precisa montar a igualdade entre razões e usar o “multiplica cruzado”.
Se 3 cadernos custam R$ 18, quanto custam 5 cadernos?
Ver solução abre/fecha
- Montando a proporção: \( \frac{3}{5} = \frac{18}{x} \).
- Multiplicando cruzado: \(3x = 90\).
- Logo: \(x = 30\).
Se você quer aprofundar a parte prática, veja também: Regra de Três (guia completo).
Aplicações de razão e proporção no cotidiano
Esse conteúdo aparece muito fora da sala de aula. Quando você entende a lógica, começa a enxergar proporções em tudo:
- 📐 Escalas de mapas e plantas
- 🍰 Receitas e misturas
- 🚗 Velocidade média
- 🛒 Comparação de preços (R$/kg, R$/L)
- 🧪 Concentração e densidade
- 🏗️ Construção (traços, medidas e projetos)
Exercícios resolvidos (mais prática)
Tente resolver antes de abrir a solução. Isso aumenta muito sua fixação.
Em um grupo, 20 pessoas são mulheres e 30 são homens. Qual a razão mulheres/homens na forma simplificada?
Ver solução abre/fecha
- Razão: \( \frac{20}{30} \).
- Simplificando por 10: \( \frac{2}{3} \).
As razões \( \frac{4}{6} \) e \( \frac{10}{15} \) formam proporção? Justifique.
Ver solução abre/fecha
- Multiplicando cruzado: \(4 \cdot 15\) e \(6 \cdot 10\).
- \(4 \cdot 15 = 60\) e \(6 \cdot 10 = 60\).
Uma impressora faz 120 páginas em 3 horas. Quantas páginas ela fará em 5 horas, mantendo o mesmo ritmo?
Ver solução abre/fecha
- Montando a proporção: \( \frac{120}{3} = \frac{x}{5} \).
- Multiplicando cruzado: \(3x = 600\).
- Logo: \(x = 200\).
Se 5 operários concluem uma obra em 18 dias, em quantos dias 6 operários (com o mesmo ritmo) concluem a mesma obra?
Ver solução abre/fecha
- Grandezas inversas (operários ↑, tempo ↓).
- Produto constante: \(5 \cdot 18 = 6 \cdot x\).
- \(90 = 6x\) → \(x = 15\).
Um atleta corre 9 km em 45 minutos. Qual a velocidade média em km/h?
Ver solução abre/fecha
- Converta 45 min para horas: \(45/60 = 0{,}75\) h.
- Velocidade: \( \frac{9}{0{,}75} = 12 \).
Para fazer um suco, mistura-se 2 partes de xarope para 6 partes de água. Qual a razão xarope/água simplificada?
Ver solução abre/fecha
- Razão: \( \frac{2}{6} \).
- Simplificando por 2: \( \frac{1}{3} \).
Complete a proporção: \( \frac{7}{x} = \frac{21}{30} \).
Ver solução abre/fecha
- Multiplicando cruzado: \(7 \cdot 30 = 21 \cdot x\).
- \(210 = 21x\).
- \(x = 10\).
Em um mapa, 1 cm representa 5 km. Qual distância real corresponde a 7 cm no mapa?
Ver solução abre/fecha
- Proporção direta: \(1 \text{ cm} \to 5 \text{ km}\).
- \(7 \text{ cm} \to x \text{ km}\).
- \(x = 7 \cdot 5 = 35\).
Um produto de 750 g custa R$ 12. Quanto custaria 1 kg, mantendo a mesma proporção?
Ver solução abre/fecha
- Proporção direta: \(750 \text{ g} \to 12\).
- \(1000 \text{ g} \to x\).
- \( \frac{750}{1000} = \frac{12}{x} \Rightarrow 750x = 12000\).
- \(x = 16\).
Duas torneiras enchem um tanque em 9 horas. Em quanto tempo 3 torneiras iguais enchem o mesmo tanque?
Ver solução abre/fecha
- Grandezas inversas (torneiras ↑, tempo ↓).
- Produto constante: \(2 \cdot 9 = 3 \cdot x\).
- \(18 = 3x \Rightarrow x = 6\).
Erros comuns em provas
- Montar a proporção com grandezas “trocadas” (invertendo sem perceber).
- Confundir direta com inversa (especialmente em problemas de tempo e trabalhadores).
- Esquecer de simplificar (a banca adora alternativas com frações não simplificadas).
- Não cuidar das unidades (minutos vs horas, gramas vs quilos).
Links internos (para continuar estudando)
Se você quer avançar com a mesma linha de raciocínio, aqui estão conteúdos que combinam muito com este tema:
- Regra de Três (guia completo)
- Porcentagem (do básico ao avançado)
- Ordem das Operações (prioridades)
- Análise Combinatória
- Estatística (conceitos essenciais)
Se algum desses links ainda não estiver publicado, você pode trocar pelo seu URL final quando for publicar.
Produtos do Matemática Hoje (para acelerar seus estudos)
Se você quer revisar mais rápido e ter material organizado para estudar todo dia, aqui estão as opções do Matemática Hoje:
Conteúdo visual para fixar fórmulas e ideias-chave em poucos minutos.
AcessarMateriais para estudar do básico ao avançado com organização e prática.
AcessarQuestões para ENEM, concursos e vestibulares com foco em revisão e fixação.
AcessarEntre nos canais e receba desafios, avisos e conteúdos novos.
AcessarConclusão
A razão compara grandezas. A proporção diz quando duas razões são equivalentes. Quando você domina isso, a regra de três e muitos problemas de prova ficam “automáticos”.
Se você quiser, eu também posso transformar estes exercícios em um bloco de “quiz” com alternativas A/B/C/D no seu padrão de post de questões.

























