Razões Trigonométricas de Ângulos Agudos

Razões Trigonométricas de Ângulos Agudos — guia completo com exemplos e exercícios

Razões Trigonométricas de Ângulos Agudos

Entenda, de forma simples, como funcionam as razões seno, cosseno e tangente — e as recíprocas cosecante, secante e cotangente. Veja também Teorema de Pitágoras, relações em ângulos complementares, exemplos passo a passo e exercícios com solução em toggle.

Navegação rápida: Definições · Teorema de Pitágoras · Razões recíprocas · Ângulos complementares · Exemplos · Exercícios

Introdução

Em um triângulo retângulo, as razões trigonométricas relacionam os comprimentos dos lados a um ângulo agudo. Elas aparecem na geometria, física, navegação, topografia e em provas como o ENEM Matemática.

SEO — termos relacionados: razões trigonométricas, seno, cosseno, tangente, triângulo retângulo, Teorema de Pitágoras, operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais, matemática básica, jogo de sinais.

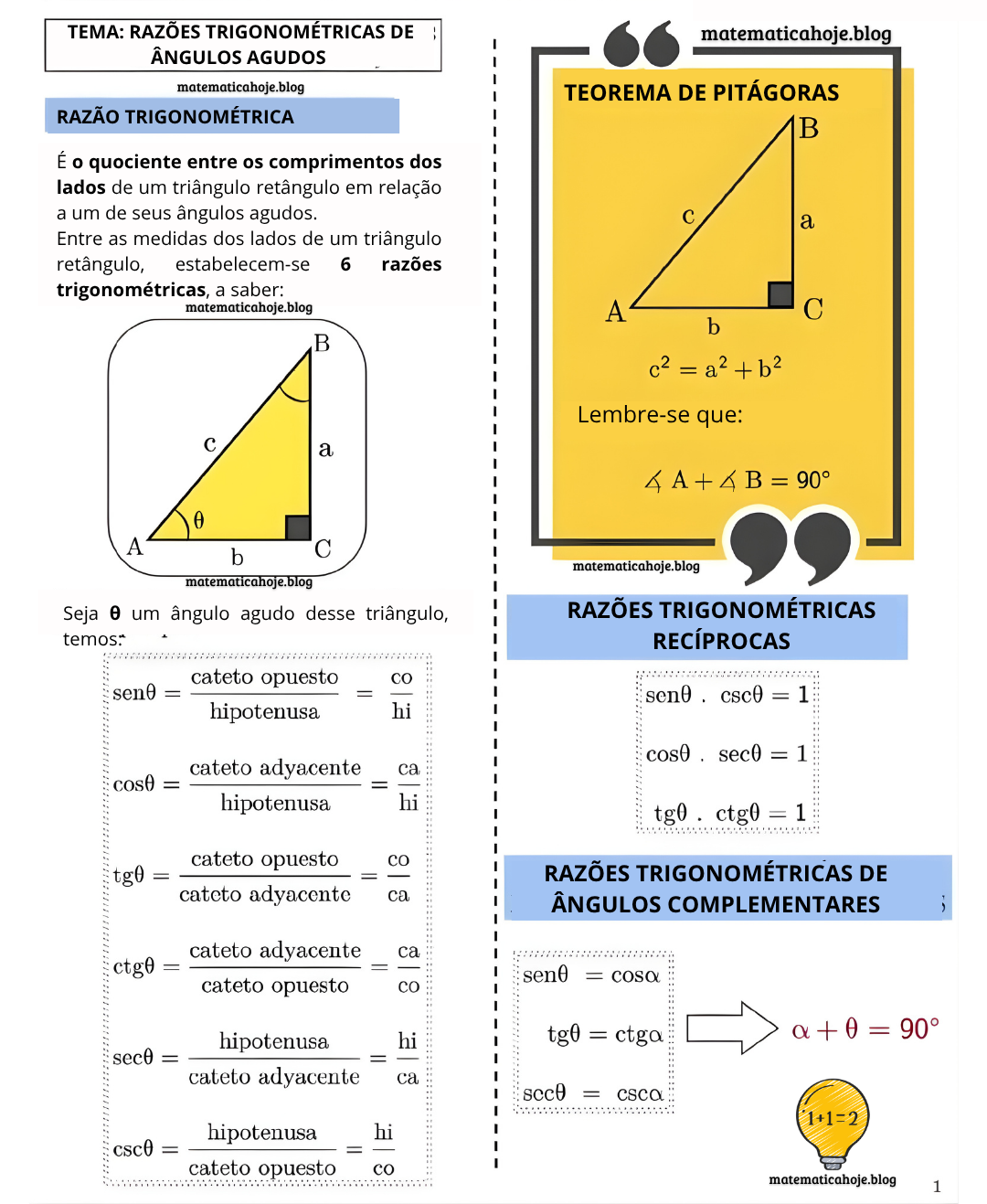
Infográfico: Razões trigonométricas de ângulos agudos

Definições (em função do ângulo \(\theta\))

\[ \begin{aligned} \sin\theta &= \frac{\text{cateto oposto}}{\text{hipotenusa}} \\ \cos\theta &= \frac{\text{cateto adjacente}}{\text{hipotenusa}} \\ \tan\theta &= \frac{\text{cateto oposto}}{\text{cateto adjacente}} \end{aligned} \]
\[ \begin{aligned} \csc\theta &= \frac{\text{hipotenusa}}{\text{cateto oposto}} \\ \sec\theta &= \frac{\text{hipotenusa}}{\text{cateto adjacente}} \\ \cot\theta &= \frac{\text{cateto adjacente}}{\text{cateto oposto}} \end{aligned} \]

Dica de memorização: SOH-CAH-TOA — Sine = Opposite / Hypotenuse, Cosine = Adjacent / Hypotenuse, Tangent = Opposite / Adjacent.

Teorema de Pitágoras

\[ c^2 = a^2 + b^2 \]

No triângulo retângulo, \(c\) é a hipotenusa e \((a,b)\) são os catetos.

Razões recíprocas

\[ \begin{aligned} \sin\theta\cdot\csc\theta &= 1 \\ \cos\theta\cdot\sec\theta &= 1 \\ \tan\theta\cdot\cot\theta &= 1 \end{aligned} \]

Ângulos complementares

Se \(\alpha+\theta=90^\circ\), então:

\[ \begin{aligned} \sin\theta &= \cos\alpha \\ \tan\theta &= \cot\alpha \\ \sec\theta &= \csc\alpha \end{aligned} \]

📌 Aprenda mais rápido com Mapas Mentais

Baixe os Mapas Mentais de Matemática e fixe fórmulas de trigonometria, geometria, PA/PG e muito mais.

Acessar Mapas Mentais

Exemplos resolvidos (passo a passo)

Exemplo 1 — Determine \(\sin\theta\), \(\cos\theta\) e \(\tan\theta\)

Num triângulo retângulo, o cateto oposto mede 6 cm e o cateto adjacente 8 cm.

Solução Pelo Teorema de Pitágoras: \( c^2 = a^2 + b^2 \) \( c^2 = 6^2 + 8^2 \) \( c^2 = 36 + 64 \) \( c^2 = 100 \) \( c = 10 \)\( \sin\theta = \frac{6}{10} = 0{,}6 \) \( \cos\theta = \frac{8}{10} = 0{,}8 \) \( \tan\theta = \frac{6}{8} = \frac{3}{4} = 0{,}75 \)

Exemplo 2 — Relação de complementares

Se \(\alpha+\theta=90^\circ\) e \(\sin\theta=\tfrac{3}{5}\), encontre \(\cos\alpha\) e \(\tan\alpha\).

Solução \( \cos\alpha = \sin\theta = \frac{3}{5} \)\( \cos\theta = \sqrt{1-\sin^2\theta} \) \( \cos\theta = \sqrt{1-\left(\frac{3}{5}\right)^2} \) \( \cos\theta = \sqrt{\frac{16}{25}} = \frac{4}{5} \) \( \tan\theta = \frac{\frac{3}{5}}{\frac{4}{5}} = \frac{3}{4} \) \( \tan\alpha = \frac{1}{\tan\theta} = \frac{4}{3} \)

Exemplo 3 — Aplicação (rampa)

Uma rampa possui altura de 1,2 m e base de 4 m. Qual é o ângulo de inclinação \(\theta\)?

Solução \( \tan\theta = \frac{1{,}2}{4} = 0{,}3 \) \( \theta = \arctan(0{,}3) \approx 16{,}70^\circ \)

🎁 Baixe grátis o eBook de Fórmulas Matemáticas

Todas as fórmulas de trigonometria em um único PDF para revisão rápida.

Quero baixar grátis

Exercícios

Seleção com itens discursivos e de múltipla escolha. Abra para ver a solução passo a passo.

1) Discursiva — calcule as três razões

No triângulo retângulo, \(co=9\) e \(ca=12\). Encontre \(\sin\theta\), \(\cos\theta\) e \(\tan\theta\).

Mostrar solução
\( c^2 = 9^2 + 12^2 \) \( c^2 = 81 + 144 \) \( c^2 = 225 \) \( c = 15 \)\( \sin\theta = \frac{9}{15} = \frac{3}{5} \) \( \cos\theta = \frac{12}{15} = \frac{4}{5} \) \( \tan\theta = \frac{9}{12} = \frac{3}{4} \)

2) Múltipla escolha — encontre \(\theta\)

Se \(\sin\theta = 0{,}8\), então \(\theta\) é aproximadamente:

  • A) \(36^\circ\)
  • B) \(47^\circ\)
  • C) \(53^\circ\)
  • D) \(64^\circ\)
Ver gabarito e solução
\( \theta = \arcsin(0{,}8) \) \( \theta \approx 53^\circ \) Alternativa correta: **C**.

3) Contexto — altura de um prédio

De um ponto no solo, observa-se o topo de um prédio sob \(\theta=40^\circ\). A distância horizontal é 25 m. Estime a altura \(h\).

Mostrar solução
\( \tan 40^\circ = \frac{h}{25} \) \( h = 25 \cdot \tan 40^\circ \) \( h \approx 25 \cdot 0{,}8391 \) \( h \approx 20{,}98\ \text{m} \)

4) Múltipla escolha — complementares

Se \(\alpha+\theta=90^\circ\) e \(\cos\theta=\tfrac{5}{13}\), então \(\sin\alpha\) é:

  • A) \(\tfrac{5}{13}\)
  • B) \(\tfrac{12}{13}\)
  • C) \(\tfrac{13}{5}\)
  • D) \(\tfrac{5}{12}\)
Ver gabarito e solução
\( \sin\alpha = \cos\theta \) \( \sin\alpha = \frac{5}{13} \) Alternativa correta: **A**.

5) Discursiva — use as recíprocas

Dado \(\sec\theta=\tfrac{13}{12}\), determine \(\cos\theta\) e \(\tan\theta\).

Mostrar solução
\( \cos\theta = \frac{1}{\sec\theta} = \frac{12}{13} \)\( \sin\theta = \sqrt{1-\cos^2\theta} \) \( \sin\theta = \sqrt{1-\left(\frac{12}{13}\right)^2} \) \( \sin\theta = \sqrt{\frac{25}{169}} = \frac{5}{13} \) \( \tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12} \)

6) Contexto — rampa de acessibilidade

Uma rampa não pode ultrapassar \(\theta=8{,}5^\circ\). Para vencer um desnível de 0,45 m, qual o comprimento mínimo?

Mostrar solução
\( \sin\theta = \frac{\text{altura}}{\text{hipotenusa}} \) \( \text{hipotenusa} = \frac{0{,}45}{\sin 8{,}5^\circ} \) \( \text{hipotenusa} \approx \frac{0{,}45}{0{,}148} \) \( \text{hipotenusa} \approx 3{,}04\ \text{m} \)

Continue estudando

Conclusão

Você revisou as seis razões trigonométricas, o Teorema de Pitágoras e as relações de ângulos complementares e recíprocas. Com prática, os cálculos ficam automáticos e você ganha rapidez em problemas de geometria e física.

Quer acelerar sua revisão? Baixe o eBook gratuito de Fórmulas e siga o canal do WhatsApp do blog para receber materiais exclusivos e novos exercícios.

Relacionadas

Área do Trapézio

Triângulo Retângulo

Fórmula de Heron

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube