Razões Trigonométricas no Triângulo Retângulo
As razões trigonométricas relacionam os lados de um triângulo retângulo com seus ângulos agudos. Neste guia, você aprende seno, cosseno e tangente com exemplos e exercícios.
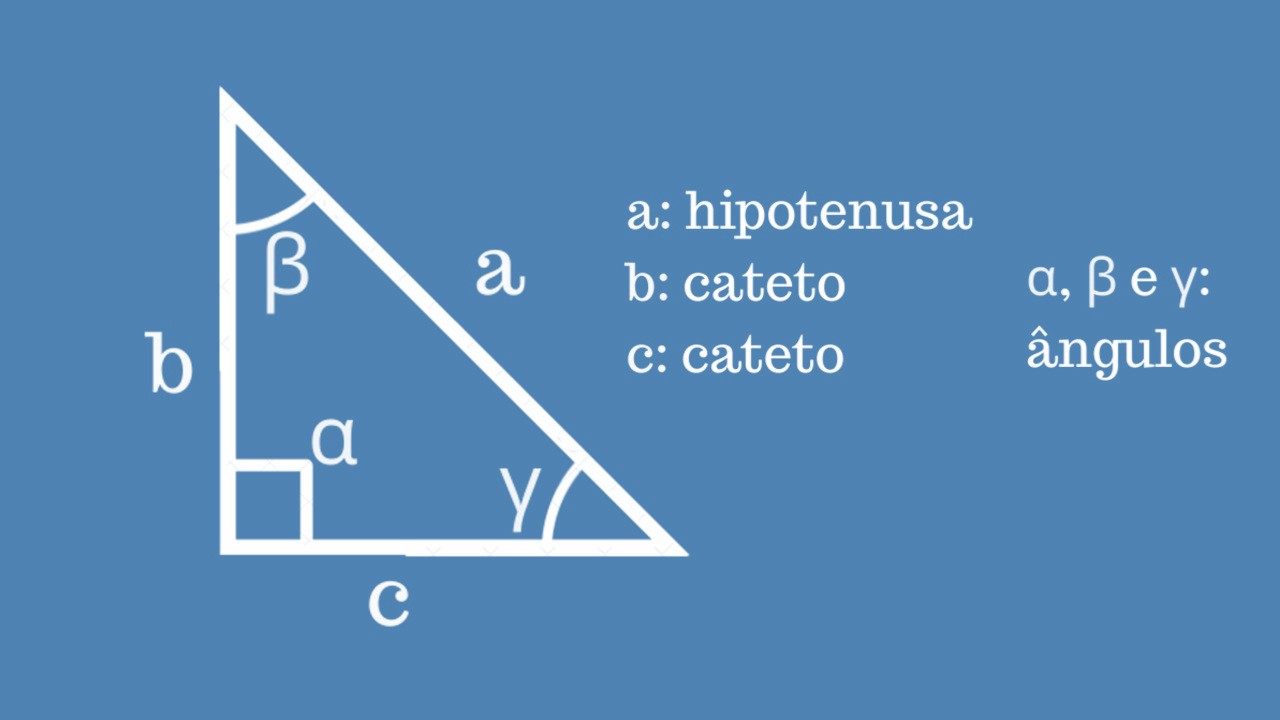
Definições (ângulo β oposto ao cateto b)
- \(\displaystyle \operatorname{sen}(β)=\frac{\text{cateto oposto}}{\text{hipotenusa}}=\frac{b}{a}\)
- \(\displaystyle \operatorname{cos}(β)=\frac{\text{cateto adjacente}}{\text{hipotenusa}}=\frac{c}{a}\)
- \(\displaystyle \operatorname{tg}(β)=\frac{\text{cateto oposto}}{\text{cateto adjacente}}=\frac{b}{c}\)
Fórmulas úteis
\(\operatorname{sen}(β)=\dfrac{b}{a}\)
\(\operatorname{cos}(β)=\dfrac{c}{a}\)
\(\operatorname{tg}(β)=\dfrac{b}{c}\)
Relações fundamentais:
\(\operatorname{sen}^2(β)+\operatorname{cos}^2(β)=1\)
\(\operatorname{tg}(β)=\dfrac{\operatorname{sen}(β)}{\operatorname{cos}(β)}\)
Exemplos resolvidos
Exemplo 1 Seno e cosseno
Para \(a=13\), \(b=5\), \(c=12\) (triângulo 5–12–13):
\(\operatorname{sen}(β)=\dfrac{5}{13}\approx0{,}3846\)
\(\operatorname{cos}(β)=\dfrac{12}{13}\approx0{,}9231\)
Verificando: \(\operatorname{sen}^2+\operatorname{cos}^2\approx0{,}148+0{,}852=1\).
Exemplo 2 Tangente
\(\operatorname{tg}(β)=\dfrac{b}{c}=\dfrac{5}{12}\approx0{,}4167\)
E também \(\operatorname{tg}(β)=\dfrac{\operatorname{sen}(β)}{\operatorname{cos}(β)}=\dfrac{5/13}{12/13}=5/12\).
Exercícios para praticar
1) Seno e cosseno
Num triângulo retângulo com \(a=10\), \(b=6\), \(c=8\), calcule \(\operatorname{sen}(β)\) e \(\operatorname{cos}(β)\).
Ver solução
\(\operatorname{sen}(β)=6/10=0{,}6\), \(\operatorname{cos}(β)=8/10=0{,}8\).
2) Tangente
Para \(a=15\), \(b=9\), \(c=12\), determine \(\operatorname{tg}(β)\) e verifique \(\operatorname{tg}=\operatorname{sen}/\operatorname{cos}\).
Ver solução
\(\operatorname{tg}(β)=9/12=0{,}75\).
\(\operatorname{sen}(β)=9/15=0{,}6\), \(\operatorname{cos}(β)=12/15=0{,}8\) → \(0{,}6/0{,}8=0{,}75\).
3) Determinar lado com razão
Se \(\operatorname{cos}(β)=0{,}8\) e \(a=25\), encontre \(c\) e \(b\).
Ver solução
\(c=\operatorname{cos}(β)\cdot a=0{,}8\cdot25=20\). Pelo Pitágoras: \(b=\sqrt{a^2-c^2}=\sqrt{625-400}=15\).
Leituras relacionadas
Continue estudando com nossos materiais premium
Lista de Exercícios — Razões Trigonométricas no Triângulo Retângulo
Resolva os exercícios abaixo e teste seus conhecimentos sobre seno, cosseno e tangente. As respostas corretas estão disponíveis no sistema de abre/fecha.
1) Cálculo básico do seno
Em um triângulo retângulo, a hipotenusa mede \(10\) cm e o cateto oposto ao ângulo \(\beta\) mede \(6\) cm. Calcule \(\operatorname{sen}(\beta)\).
- A) 0,4
- B) 0,5
- C) 0,6
- D) 0,8
- E) 1,0
Ver solução
\(\operatorname{sen}(\beta)=\dfrac{\text{cateto oposto}}{\text{hipotenusa}}\) \(\operatorname{sen}(\beta)=\dfrac{6}{10}=0,6\). Alternativa correta: C
2) Determinando o cosseno
No mesmo triângulo do exercício anterior, o cateto adjacente ao ângulo \(\beta\) mede \(8\) cm. Calcule \(\operatorname{cos}(\beta)\).
- A) 0,4
- B) 0,6
- C) 0,7
- D) 0,8
- E) 1,0
Ver solução
\(\operatorname{cos}(\beta)=\dfrac{\text{cateto adjacente}}{\text{hipotenusa}}\) \(\operatorname{cos}(\beta)=\dfrac{8}{10}=0,8\). Alternativa correta: D
3) Tangente do ângulo
Um triângulo retângulo possui catetos \(5\) cm e \(12\) cm. Calcule \(\operatorname{tg}(\beta)\) para o ângulo oposto ao cateto de \(5\) cm.
- A) 0,36
- B) 0,41
- C) 0,5
- D) 0,83
- E) 1,2
Ver solução
\(\operatorname{tg}(\beta)=\dfrac{\text{cateto oposto}}{\text{cateto adjacente}}\) \(\operatorname{tg}(\beta)=\dfrac{5}{12}\approx0,4167\). Alternativa correta: B
4) Determinando um cateto usando seno
Em um triângulo retângulo, \(\operatorname{sen}(\beta)=0,6\) e a hipotenusa mede \(25\) cm. Qual o valor do cateto oposto?
- A) 10 cm
- B) 12 cm
- C) 15 cm
- D) 18 cm
- E) 20 cm
Ver solução
\(\operatorname{sen}(\beta)=\dfrac{\text{cateto oposto}}{\text{hipotenusa}}\) \(0,6=\dfrac{x}{25}\implies x=0,6\cdot25=15\ \text{cm}\). Alternativa correta: C
5) Determinando ângulo com cosseno
Um triângulo retângulo possui \(\operatorname{cos}(\beta)=0,8\). Determine o valor aproximado de \(\beta\) em graus.
- A) \(30^\circ\)
- B) \(36^\circ\)
- C) \(40^\circ\)
- D) \(45^\circ\)
- E) \(53^\circ\)
Ver solução
\(\beta=\arccos(0,8)\) \(\beta\approx36,87^\circ\). Alternativa correta: B
6) Relação fundamental
Para um triângulo retângulo com \(\operatorname{sen}(\beta)=0,6\), verifique \(\operatorname{cos}(\beta)\) usando a relação \(\operatorname{sen}^2+\operatorname{cos}^2=1\).
- A) 0,6
- B) 0,7
- C) 0,8
- D) 0,9
- E) 1,0
Ver solução
\(\operatorname{cos}^2=1-\operatorname{sen}^2=1-(0,6)^2=1-0,36=0,64\) \(\operatorname{cos}=\sqrt{0,64}=0,8\). Alternativa correta: C
7) Determinando a hipotenusa
Num triângulo retângulo, \(\operatorname{tg}(\beta)=0,75\) e o cateto adjacente mede \(12\) cm. Calcule a hipotenusa.
- A) 15 cm
- B) 16 cm
- C) 18 cm
- D) 20 cm
- E) 25 cm
Ver solução
\(\operatorname{tg}(\beta)=\dfrac{b}{c}=0,75\) \(b=0,75\cdot c=0,75\cdot12=9\ \text{cm}\) \(a=\sqrt{b^2+c^2}=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15\ \text{cm}\). Alternativa correta: A
8) Aplicando seno para encontrar altura
Uma escada forma um ângulo de \(30^\circ\) com o chão e encosta na parede a \(3\) m de altura. Qual o comprimento da escada?
- A) 4 m
- B) 5 m
- C) 6 m
- D) 7 m
- E) 8 m
Ver solução
\(\operatorname{sen}(30^\circ)=\dfrac{3}{a}\) \(\dfrac{1}{2}=\dfrac{3}{a}\implies a=\dfrac{3}{1/2}=6\ \text{m}\). Alternativa correta: C
9) Problema contextualizado
Um avião levanta voo com inclinação de \(20^\circ\) em relação ao solo. Após percorrer \(300\) m de pista, qual a altura atingida?
- A) 80 m
- B) 90 m
- C) 100 m
- D) 105 m
- E) 110 m
Ver solução
\(\operatorname{sen}(20^\circ)=\dfrac{h}{300}\) \(h=300\cdot\operatorname{sen}(20^\circ)\) \(h\approx300\cdot0,342=102,6\ \text{m}\approx103\ \text{m}\). Alternativa correta: D
10) Questão avançada
Um observador vê o topo de um prédio sob um ângulo de \(60^\circ\). Sabendo que ele está a \(50\) m da base, calcule a altura do prédio.
- A) 75 m
- B) 80 m
- C) 85 m
- D) 86,6 m
- E) 90 m
Ver solução
\(\operatorname{tg}(60^\circ)=\dfrac{h}{50}\) \(\sqrt{3}=\dfrac{h}{50}\) \(h=50\sqrt{3}\approx50\cdot1,732=86,6\ \text{m}\). Alternativa correta: D













