Relação entre Tangente, Seno e Cosseno

A identidade \( \tan\alpha=\dfrac{\sin\alpha}{\cos\alpha} \) conecta diretamente as três razões trigonométricas mais usadas. Ela vale para qualquer ângulo para o qual \( \cos\alpha\neq0 \) e é onipresente em problemas de geometria, trigonometria e física.

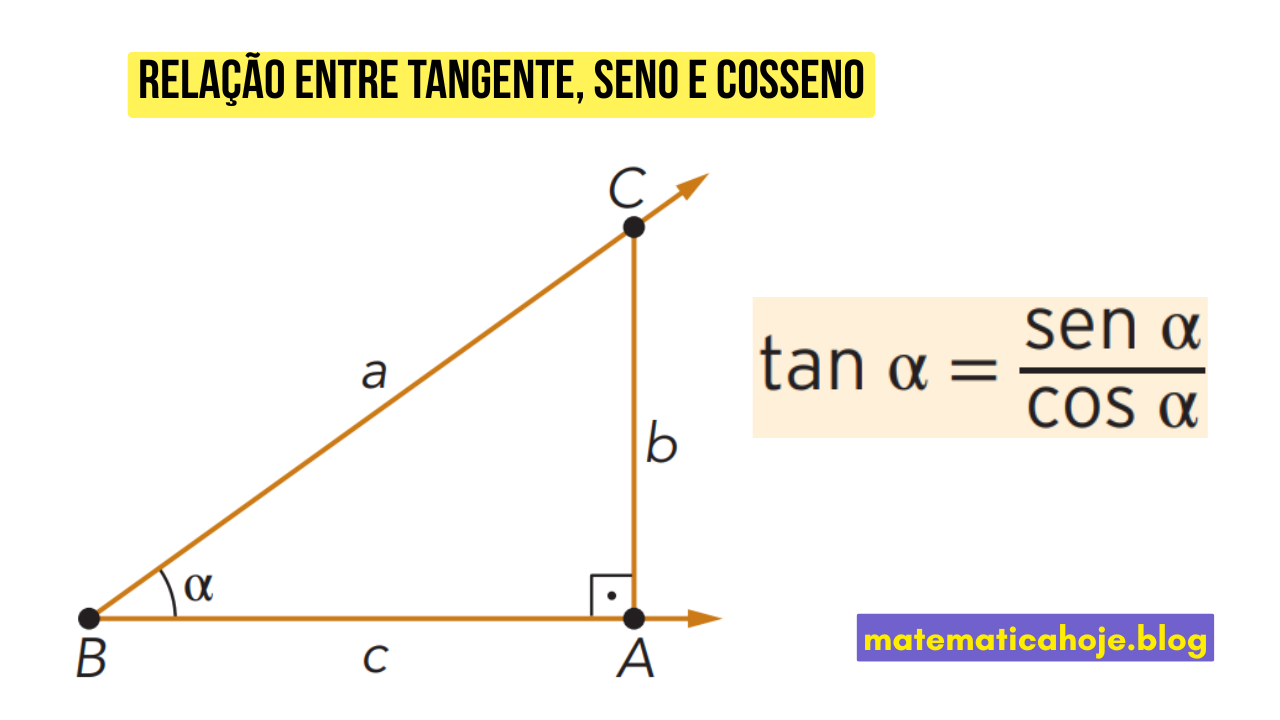
1) No triângulo retângulo

Seja um triângulo retângulo com ângulo agudo \( \alpha \). Por definição:

\( \sin\alpha = \dfrac{\text{cateto oposto}}{\text{hipotenusa}} = \dfrac{b}{a} \)
\( \cos\alpha = \dfrac{\text{cateto adjacente}}{\text{hipotenusa}} = \dfrac{c}{a} \)
\( \tan\alpha = \dfrac{\text{oposto}}{\text{adjacente}} = \dfrac{b}{c} \)

\[ \frac{\sin\alpha}{\cos\alpha}=\frac{\frac{b}{a}}{\frac{c}{a}}=\frac{b}{c}=\tan\alpha. \]

A igualdade surge ao dividir seno por cosseno: a hipotenusa cancela e sobra a razão oposto/adjacente.

2) No círculo trigonométrico

No plano, para um ponto \(P(\cos\alpha,\sin\alpha)\) do círculo unitário, a reta tangente em \(x=1\) intercepta a semirreta que forma o ângulo \( \alpha \) no ponto \(T(1,\tan\alpha)\). O coeficiente angular é \( \tan\alpha = \dfrac{\sin\alpha}{\cos\alpha} \) (quando \( \cos\alpha\neq0 \)).

3) Consequências úteis

\( \tan^2\alpha = \dfrac{\sin^2\alpha}{\cos^2\alpha} \). Com a identidade fundamental \( \sin^2\alpha+\cos^2\alpha=1 \), deduz-se \( 1+\tan^2\alpha=\dfrac{1}{\cos^2\alpha}=\sec^2\alpha \).
Simplificação de expressões: transformar tangente em \( \sin/\cos \) costuma facilitar somas, produtos e equações.

4) Exemplos resolvidos

Exemplo 1: Dado \( \cos\alpha=\frac{3}{5} \) e \( \alpha \) agudo, calcule \( \tan\alpha \).

\( \sin\alpha=\sqrt{1-\cos^2\alpha}=\sqrt{1-\frac{9}{25}}=\frac{4}{25^{1/2}}=\frac{4}{5} \). Logo, \( \tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{4/5}{3/5}=\dfrac{4}{3} \).

Exemplo 2: Resolva \( \tan\alpha=\dfrac{3}{4} \) com \( \alpha \) agudo. Encontre \( \sin\alpha \) e \( \cos\alpha \).

Interprete como triângulo com oposto \(3k\) e adjacente \(4k\), hipotenusa \(5k\). Assim, \( \sin\alpha=\dfrac{3}{5} \) e \( \cos\alpha=\dfrac{4}{5} \).

📘 Exercícios (múltipla escolha) — com solução

1) Se \( \sin\alpha=\dfrac{5}{13} \) e \( \alpha \) é agudo, então \( \tan\alpha=\)

\(\dfrac{5}{12}\)
\(\dfrac{5}{12}\)
\(\dfrac{12}{5}\)
\(\dfrac{13}{12}\)

Ver solução

\( \cos\alpha=\sqrt{1-\frac{25}{169}}=\frac{12}{13} \Rightarrow \tan\alpha=\frac{5/13}{12/13}=\frac{5}{12}. \)

2) Sabendo que \( \cos\alpha=0{,}8 \) e \( \alpha \) é agudo, o valor de \( \tan\alpha \) é:

0,6
1,25
0,75
1,5

Ver solução

\( \sin\alpha=\sqrt{1-0{,}8^2}=\sqrt{0{,}36}=0{,}6 \Rightarrow \tan\alpha=\frac{0{,}6}{0{,}8}=0{,}75. \)

3) Se \( \tan\alpha=\dfrac{7}{24} \), quais são \( \sin\alpha \) e \( \cos\alpha \) (com \( \alpha \) agudo)?

\(\dfrac{7}{25},\ \dfrac{24}{25}\)
\(\dfrac{7}{25},\ \dfrac{24}{25}\)
\(\dfrac{24}{25},\ \dfrac{7}{25}\)
\(\dfrac{7}{24},\ \dfrac{1}{25}\)

Ver solução

Triângulo 7–24–25 ⇒ \( \sin=\frac{7}{25} \), \( \cos=\frac{24}{25} \).

4) Simplifique \( \dfrac{\tan\alpha}{\sin\alpha} \) (com \( \cos\alpha\neq0 \)).

\(\sec\alpha\)
\(\cos\alpha\)
\(\dfrac{1}{\cos\alpha}\)
\(\sin\alpha\)

Ver solução

\( \frac{\tan\alpha}{\sin\alpha}=\frac{\sin\alpha/\cos\alpha}{\sin\alpha}=\frac{1}{\cos\alpha}=\sec\alpha. \)

5) Resolva \( \tan\alpha=\dfrac{\sin\alpha}{2} \) para \( \alpha \) agudo.

\( \cos\alpha=2 \)
\( \sin\alpha=0 \)
\( \cos\alpha=\dfrac{1}{2} \Rightarrow \alpha=60^\circ \)
\( \sin\alpha=\dfrac{1}{2} \Rightarrow \alpha=30^\circ \)

Ver solução

Substitua \( \tan=\sin/\cos \): \( \dfrac{\sin\alpha}{\cos\alpha}=\dfrac{\sin\alpha}{2} \Rightarrow \sin\alpha\neq0 \) (pois agudo) e então \( \dfrac{1}{\cos\alpha}=\dfrac{1}{2} \Rightarrow \cos\alpha=\dfrac{1}{2} \Rightarrow \alpha=60^\circ \).