Segmento Circular
O segmento circular é a região do círculo limitada por uma corda e pelo arco correspondente. Nesta página, reunimos fórmulas (em radianos e graus), relações com corda e flecha/sagita, exemplos resolvidos e exercícios.
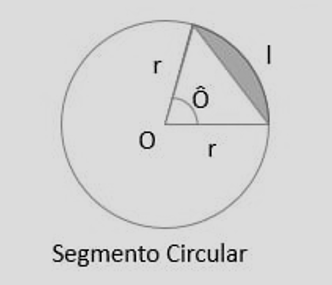
Definição e elementos
- Raio \(r\), ângulo central \(\theta\) (em radianos) ou \(\alpha\) (em graus).
- Corda \(c\) que delimita o segmento com o arco.
- Flecha (sagita) \(h\): distância do meio da corda ao arco (na direção do centro).
Fórmulas essenciais
Útil quando você mede a flecha \(h\) diretamente.
Exemplos resolvidos (passo a passo)
1) Área do segmento pelo ângulo (graus)
Em um círculo de raio \(r=10\,\text{cm}\), a corda subtende um ângulo central \(\alpha=72^\circ\). Calcule \(A_{\text{seg}}\).
Ver solução
2) Área do segmento pela flecha
Um arco em um círculo de raio \(r=12\,\text{cm}\) tem flecha \(h=2{,}5\,\text{cm}\). Encontre \(A_{\text{seg}}\).
Ver solução
3) Comparando setor e triângulo (definição clássica)
Mostre que \(A_{\text{seg}}=A_{\text{set}}-A_{\triangle}\) para um segmento determinado por \(\theta\) (rad) em um círculo de raio \(r\).
Ver solução
Exercícios resolvidos
(E1) Segmento por ângulo em radianos
Num círculo de raio \(r=8\,\text{cm}\), a abertura é \(\theta=1{,}1\,\text{rad}\). Calcule a área do segmento.
Ver solução
(E2) Segmento por ângulo em graus
Para \(r=15\,\text{cm}\) e \(\alpha=40^\circ\), determine \(A_{\text{seg}}\).
Ver solução
(E3) Segmento a partir da flecha
Um arco de raio \(r=20\,\text{cm}\) tem flecha \(h=3\,\text{cm}\). Encontre \(A_{\text{seg}}\).
Ver solução
Continue estudando (linkagem interna)
- Área do Círculo — base para todas as áreas envolvendo raios.
- Área do Setor Circular — necessário para deduzir o segmento via \(A_{\text{set}}-A_{\triangle}\).
- Raio, Diâmetro e Cordas — relações \(c=2r\sin(\alpha/2)\) e flecha.
- Comprimento da Circunferência — arcos \(L=r\theta\) e proporção em graus.
Materiais do Matemática Hoje
Quer revisar com mapas e listas? Veja: