Seno e Cosseno nos Ângulos Notáveis: 0°, 90°, 180°, 270° e 360°
Na circunferência trigonométrica, a cada número real \(t\) associamos o ponto \(P(t)=(\cos t,sen t)\). Os cinco ângulos de eixo — \(0^\circ, 90^\circ, 180^\circ, 270^\circ\) e \(360^\circ\) — são referências que simplificam cálculos e esboços de gráficos trigonométricos.
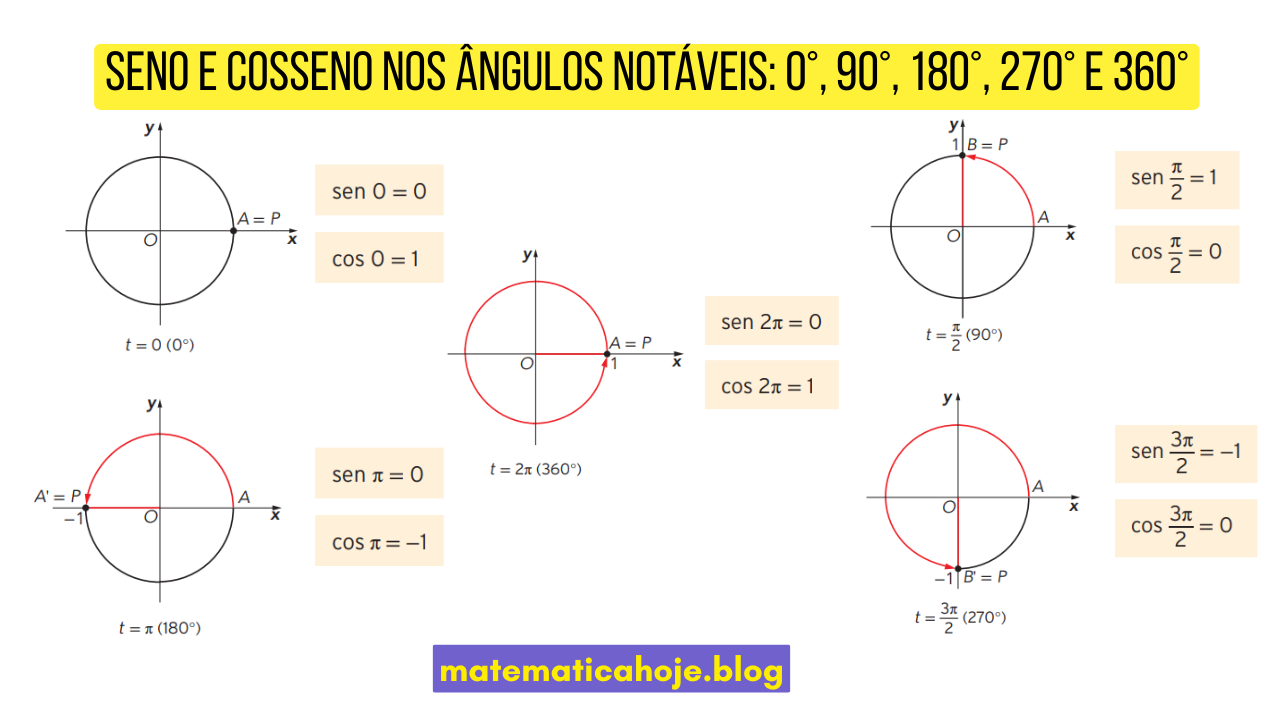
Valores nos cinco ângulos de referência
| Ângulo | \(\cos t\) | \(sen t\) | Ponto \(P(t)\) |
|---|---|---|---|
| \(0^\circ\) ou \(0\) | \(1\) | \(0\) | \((1,0)\) |
| \(90^\circ\) ou \(\dfrac{\pi}{2}\) | \(0\) | \(1\) | \((0,1)\) |
| \(180^\circ\) ou \(\pi\) | \(-1\) | \(0\) | \((-1,0)\) |
| \(270^\circ\) ou \(\dfrac{3\pi}{2}\) | \(0\) | \(-1\) | \((0,-1)\) |
| \(360^\circ\) ou \(2\pi\) | \(1\) | \(0\) | \((1,0)\) |
Interpretação geométrica
\(\cos t\) é a abscissa (coordenada \(x\)) e \(sen t\) é a ordenada (coordenada \(y\)) do ponto \(P(t)\) na circunferência de raio 1.
Periocidade
Para qualquer \(t\in\mathbb{R}\): \(\cos(t+2\pi)=\cos t\) e \(sen(t+2\pi)=sen t\). Por isso \(0\) e \(2\pi\) têm os mesmos valores.
Relação fundamental
Em todos os casos, vale \(sen^2 t+\cos^2 t=1\), pois os pontos pertencem à circunferência de raio 1 centrada na origem.
Exercícios de múltipla escolha
1) \(sen(450^\circ)\) e \(\cos(450^\circ)\) valem, respectivamente:
- \((0,1)\)
- \((1,0)\)
- \((0,-1)\)
- \((-1,0)\)
Ver solução
\(450^\circ=360^\circ+90^\circ\Rightarrow\) coincide com \(90^\circ\). Logo \(sen=1\) e \(\cos=0\). Alternativa B.
2) No intervalo \(0\le t\le 2\pi\), onde \(sen t\) atinge valor mínimo?
- \(0\)
- \(\dfrac{\pi}{2}\)
- \(\pi\)
- \(\dfrac{3\pi}{2}\)
Ver solução
Em \(3\pi/2\), \(sen t=-1\) (mínimo). Alternativa D.
3) O par \((\cos t,sen t)\) para \(t=\dfrac{7\pi}{2}\) é:
- \((1,0)\)
- \((0,1)\)
- \((0,-1)\)
- \((-1,0)\)
Ver solução
\(\dfrac{7\pi}{2}=2\pi+\dfrac{3\pi}{2}\Rightarrow\) coincide com \(3\pi/2\). Logo \((0,-1)\). Alternativa C.
4) Assinale a correta:
- \(\cos 0=\cos \pi\)
- \(sen \pi=sen 2\pi\)
- \(\cos 0=\cos 2\pi\)
- \(sen \dfrac{\pi}{2}=-1\)
Ver solução
Somente \(\cos 0=\cos 2\pi=1\) é verdadeira. Alternativa C.
5) \(sen t=0\) ocorre em:
- \(t=\dfrac{\pi}{2}\) e \(t=\dfrac{3\pi}{2}\)
- \(t=\dfrac{\pi}{2}\) e \(t=2\pi\)
- \(t=0,\ \pi,\ 2\pi\)
- \(t=\pi\) apenas
Ver solução
Nos pontos de interseção com o eixo \(x\): \(0,\pi,2\pi\). Alternativa C.
6) O ponto \(P\big(\dfrac{3\pi}{2}\big)\) é:
- \((1,0)\)
- \((0,1)\)
- \((-1,0)\)
- \((0,-1)\)
Ver solução
Em \(3\pi/2\) estamos no eixo negativo de \(y\): \((0,-1)\). Alternativa D.
🎒 Materiais recomendados do blog
Aprofunde o estudo de circunferência trigonométrica, ângulos notáveis e funções periódicas.
Coleção 10 eBooks – Trigonometria Essencial
Teoria objetiva, exemplos resolvidos e listas graduadas com gabarito.
Mapas Mentais de Matemática
Diagramas com sinais por quadrante, ângulos notáveis e relações fundamentais.
Banco de Questões – Matemática
Centenas de itens por habilidade: leitura de \(P(t)\), valores notáveis e aplicações.
ENEM Matemática
Roteiro de estudo, resumos e baterias de exercícios focadas no exame.
Canais Oficiais de Matemática
Acompanhe novidades, listas e materiais extras nos canais verificados.






















