Você sabe o que significam os principais símbolos matemáticos?
Os símbolos matemáticos são a linguagem que permite escrevermos ideias complexas de maneira curta e precisa. Dominar seu significado acelera a leitura de enunciados, evita interpretações erradas e deixa a resolução de problemas muito mais objetiva. A seguir, você encontra uma tabela ampla e organizada por categorias com os símbolos mais usados em Aritmética, Conjuntos, Lógica, Álgebra, Geometria, Trigonometria, Cálculo, Estatística e Álgebra Linear — seguida de exemplos práticos e exercícios com solução.
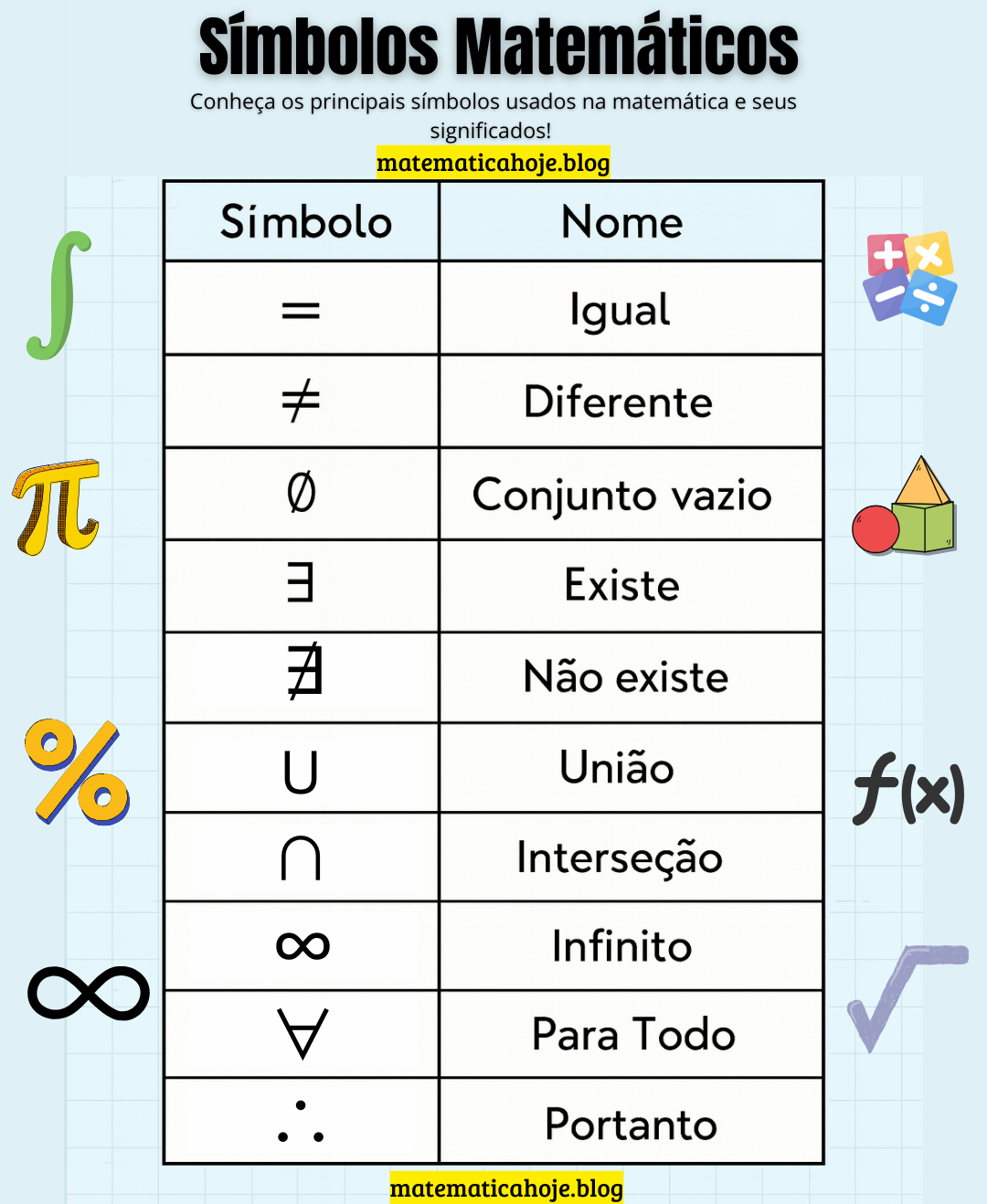
Principais símbolos: guia completo e aplicado
| Símbolo | Nome | Uso / Exemplo |
|---|---|---|
| Aritmética e relações | ||
| = | Igual | \(3+2=5\) |
| ≠ | Diferente | \(7≠10\) |
| < , ≤ | Menor; Menor ou igual | \(x<5\); \(x≤5\) |
| > , ≥ | Maior; Maior ou igual | \(x>2\); \(x≥2\) |
| ± | Mais ou menos | Raízes: \(x=±\sqrt{5}\) |
| ≈ , ≅ | Aproximadamente; Congruente | \(\pi≈3{,}14\) |
| ∣ , ∤ | Divide; Não divide | \(3∣12\); \(3∤14\) |
| √ , \(ⁿ\!\sqrt{\;\;}\) | Raiz; Raiz n-ésima | \(\sqrt{9}=3\); \(\sqrt[3]{8}=2\) |
| ! | Fatorial | \(5!=120\) |
| ⌊x⌋ , ⌈x⌉ | Piso; Teto | ⌊2,9⌋=2; ⌈2,1⌉=3 |
| Conjuntos | ||
| ∈ , ∉ | Pertence; Não pertence | \(3∈\mathbb{N}\); \(−1∉\mathbb{N}\) |
| ⊂ , ⊆ | Subconjunto; Subconjunto ou igual | \(\{1,2\}⊂\mathbb{N}\) |
| ⊄ , ⊈ | Não é subconjunto | \(\{0\}⊄\mathbb{N^+}\) |
| ⊃ , ⊇ | Superconjunto; Superconjunto ou igual | \(\mathbb{R}⊃\mathbb{Q}\) |
| ∪ , ∩ | União; Interseção | \(A∪B\); \(A∩B\) |
| \ | Diferença de conjuntos | \(A\setminus B\) |
| ∅ | Conjunto vazio | \(A∩A^c=∅\) |
| ℕ, ℤ, ℚ, ℝ, ℂ | Conjuntos numéricos | Naturais, Inteiros, Racionais, Reais, Complexos |
| 𝒫(A) | Conjunto potência | Todos os subconjuntos de \(A\) |
| |A| | Cardinalidade | Número de elementos |
| Lógica e quantificadores | ||
| ¬ | Negação | ¬\(p\) |
| ∧ , ∨ | Conjunção; Disjunção | \(p∧q\); \(p∨q\) |
| ⇒ , ⇔ | Implica; Se e somente se | \(p⇒q\); \(p⇔q\) |
| ∴ | Portanto | Conclusão de prova |
| ∀ , ∃ , ∄ | Para todo; Existe; Não existe | \(∀x\in\mathbb{R}\), \(∃x\) |
| Álgebra / Funções | ||
| f: A→B | Função | Domínio \(A\), contradomínio \(B\) |
| ∘ | Composição | \((f∘g)(x)\) |
| ≡ | Identidade / congruência | \(f(x)≡g(x)\) |
| ∝ | Proporcional a | \(y∝x\) |
| ∑ | Somatório | \(\sum_{i=1}^{n} a_i\) |
| ∏ | Produto | \(\prod_{k=1}^{n} b_k\) |
| π | Pi | Razão \(C/d\) no círculo |
| i | Unidade imaginária | \(i^2=-1\) |
| Re(z), Im(z) | Parte real e imaginária | Complexos |
| |z| | Módulo | \(|a+bi|=\sqrt{a^2+b^2}\) |
| Geometria | ||
| ∠ | Ângulo | \(∠ABC\) |
| ⊥ , ∥ | Perpendicular; Paralelo | r ⊥ s; r ∥ s |
| △ , □ , ∘ | Triângulo; Quadrado; Círculo | Figuras planas |
| ≅ , ≈ | Congruente; Semelhante | Triângulos \(≅\) / \(≈\) |
| ∼ | Semelhança | \(AB/DE = AC/DF\) |
| ◻ABCD | Polígono nomeado | Quadrilátero ABCD |
| ° , ′ , ″ | Graus; Min.; Seg. | Ângulos: 30° 15′ 20″ |
| Trigonometria | ||
| \(\sin,\cos,\tan\) | Seno, cosseno, tangente | \(\sin^2x+\cos^2x=1\) |
| \(\csc,\sec,\cot\) | Funções recíprocas | \(\sec x=1/\cos x\) |
| arcsin etc. | Funções inversas | \(y=\arcsin x\) |
| Cálculo | ||
| \(\dfrac{d}{dx}\), \(f'(x)\) | Derivada | \(\frac{d}{dx}x^2=2x\) |
| \(\dfrac{∂}{∂x}\) | Derivada parcial | Funções de várias variáveis |
| \(\int\), \(\int_a^b\) | Integral; Integral definida | \(\int x\,dx\) |
| ∇ , ∇· , ∇× | Gradiente; Divergente; Rotacional | Vetorial |
| \(\lim_{x\to a}\) | Limite | Comportamento de \(f(x)\) |
| ≈, O( ) | Aproximação; Ordem | Análise assintótica |
| ∞ | Infinito | Limites e séries |
| Estatística e probabilidade | ||
| \(\bar{x}\) | Média amostral | \(\bar{x}=\frac{1}{n}\sum x_i\) |
| \(σ, s\) | Desvio padrão populacional; amostral | Dispersão |
| \(Var(X)\) | Variância | \(Var(X)=E[(X-μ)^2]\) |
| \(P(A)\) | Probabilidade | 0 ≤ \(P(A)\) ≤ 1 |
| \(A’\) ou \(A^c\) | Complemento | Eventos |
| \(P(A|B)\) | Prob. condicional | \(=\frac{P(A∩B)}{P(B)}\) |
| \(E[X]\) | Valor esperado | Média teórica |
| \(~\) | Distribui-se como | \(X∼\mathcal{N}(μ,σ^2)\) |
| \(\binom{n}{k}\) | Coeficiente binomial | Combinações |
| Álgebra Linear | ||
| \(\vec{v}\), \(\mathbf{A}\) | Vetor; Matriz | Notação em negrito/seta |
| \(\mathbf{A}^T\) | Transposta | Troca linhas/colunas |
| \(\det(\mathbf{A})\) | Determinante | Área/volume escalar |
| \(\mathbf{A}^{-1}\) | Inversa | \(\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}\) |
| \(\mathbf{I}\) | Matriz identidade | Diagonal de 1s |
| \(\langle u,v\rangle\) | Produto interno | Ângulo e norma |
| \(\|v\|\) | Norma | Comprimento do vetor |
| \(span\{v_i\}\) | Gerado por vetores | Subespaço |
| \(λ\) | Autovalor | \(\mathbf{A}x=λx\) |
Exemplos práticos com símbolos matemáticos
1. Símbolo de igualdade (=)
Usado para indicar que dois valores ou expressões possuem o mesmo resultado.
Exemplo: \( 3 + 2 = 5 \)
2. Símbolo de diferença (≠)
Mostra que dois valores não são iguais.
Exemplo: \( 7 ≠ 5 + 1 \)
3. União e interseção (∪ e ∩)
Esses símbolos são usados em conjuntos. A união representa a junção de elementos e a interseção indica o que há em comum.
Exemplo:
\( A = \{1, 2, 3\} \)
\( B = \{3, 4, 5\} \)
\( A ∪ B = \{1, 2, 3, 4, 5\} \)
\( A ∩ B = \{3\} \)
Lista de exercícios sobre símbolos matemáticos
Enunciado: Dado \( A = \{2, 4, 6\} \) e \( B = \{4, 6, 8\} \), determine \( A ∪ B \) e \( A ∩ B \).
Solução:
\( A ∪ B = \{2, 4, 6, 8\} \)
\( A ∩ B = \{4, 6\} \)
Enunciado: Interprete: \(∀x∈\mathbb{N}, ∃y∈\mathbb{N}\) tal que \(y=x+1\).
Solução:
Para todo número natural \(x\), existe um \(y\) natural que é o sucessor de \(x\).
Conclusão
Conhecer o “alfabeto” da matemática dá fluidez às resoluções e clareza às demonstrações. Guarde esta tabela como referência rápida e use os exemplos para consolidar o entendimento. Com prática, cada símbolo se tornará natural na leitura e na escrita matemática.
Perguntas Frequentes (FAQ)
Quais símbolos não podem faltar no meu caderno de estudos?
Igual (=), diferente (≠), união (∪), interseção (∩), pertencimento (∈), somatório (∑), integral (∫), derivada (d/dx), π e ∞. Eles aparecem em quase todos os conteúdos.
Qual a diferença entre ⊂ e ⊆ em conjuntos?
Em geral, ⊂ indica “subconjunto próprio” (sem igualdade) e ⊆ permite igualdade. Alguns livros usam ⊂ como ⊆; observe a convenção do seu curso.
Quando usar ∀ e ∃ em problemas?
Use ∀ para declarações universais (“para todo x”) e ∃ quando quiser afirmar a existência de ao menos um elemento com certa propriedade (“existe x”).
Autor: Prof. Adriano Rocha — matematicahoje.blog