Superfícies de um Cone
Área lateral, área da base e área total com fórmulas, relações geométricas e exemplo resolvido.
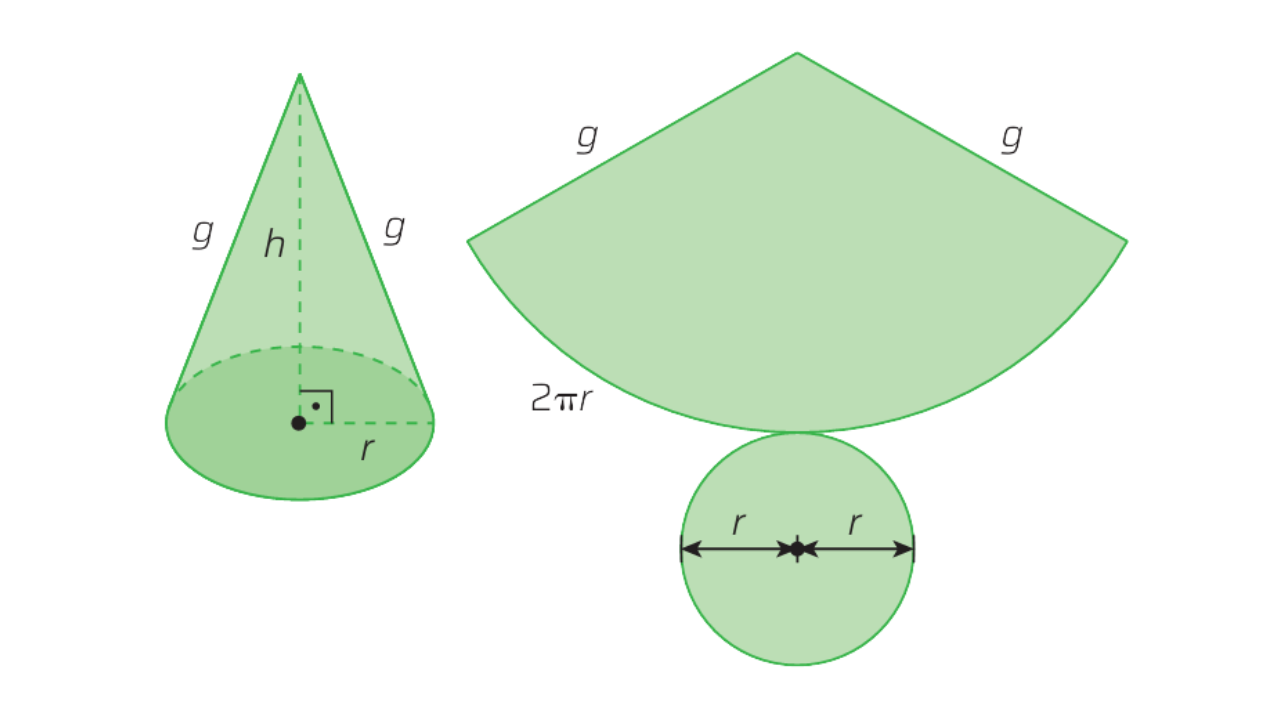
1) Elementos do cone
Base (circular) círculo de raio \(r\).
Altura \(h\) distância perpendicular do vértice ao plano da base.
Geratriz \(g\) segmento que liga o vértice a um ponto da circunferência da base.
Esses três elementos formam um triângulo retângulo, logo:
Use esta relação para encontrar qualquer um dos três quando conhecer os outros dois.
2) Superfície lateral \(S_l\)
Na planificação, a superfície lateral vira um setor circular de raio \(g\). O arco do setor é igual ao perímetro da base, isto é, \(2\pi r\).
Válida para cone reto. Se souber \(h\) em vez de \(g\), substitua \(g=\sqrt{r^2+h^2}\).
3) Superfície da base \(S_b\)
A base é um círculo de raio \(r\).
4) Superfície total \(S_t\)
É a soma da lateral com a base.
5) Exemplo resolvido
Dados: \(r=6\,\text{cm}\) e \(g=10\,\text{cm}\). Calcular a superfície total.
Mostrar a solução passo a passo
Área lateral: \(S_l=\pi r g=\pi\cdot6\cdot10=60\pi\).
Área da base: \(S_b=\pi r^2=\pi\cdot6^2=36\pi\).
Área total: \(S_t=60\pi+36\pi=96\pi\;\text{cm}^2\approx 301{,}44\;\text{cm}^2\) (com \(\pi\approx3{,}14\)).
Se o problema trouxer \(h\) em vez de \(g\), primeiro aplique \(g=\sqrt{r^2+h^2}\).
6) Dicas e aplicações
- Planificação: o setor circular tem raio \(g\) e arco \(2\pi r\).
- Unidades: áreas sempre em unidades quadradas (cm², m², …).
- Aplicações: embalagens (cone de sorvete), funis, cúpulas e arquitetura.
Continue estudando
Reforce o conteúdo com resumos visuais, listas de exercícios e materiais para revisão.






















